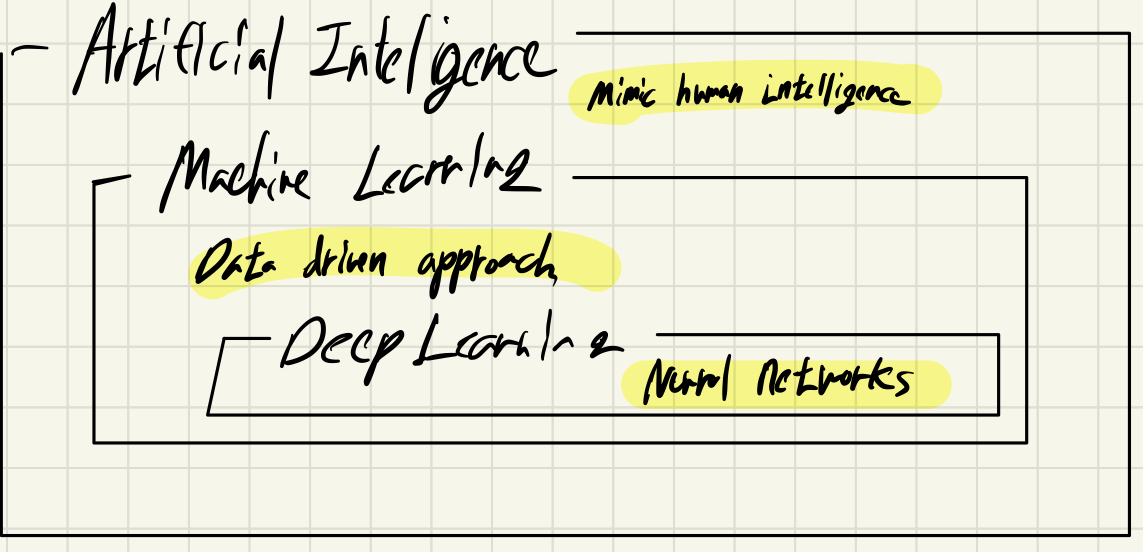
인공지능이란? (Artificial Inteligence)
사람의 지능을 모방하는 것을 말합니다. (Mimic Human Intelligence)
사람은 최선이라 생각하는 의사 결정을 수행하고, 행동으로 옮깁니다. 마찬가지로 최선이라고 여겨지는 알고리즘을 채택하여 결과를 도출하는 것을 인공지능이라 하는 것 같습니다.
머신러닝이란? (Machine Learning)
인공지능에는 다양한 기술들이 있고, 그 가운데 Data를 기반으로 문제에 접근하는 방식을 기계 학습이라고 할 수 있습니다. (Data Driven Approach)
딥러닝이란? (Deep Learning)
hierarchical representation learning 이라고 말할 수 있습니다. 쉽게 이해하자면,
Neural Networks 를 Deep 하게 쌓아 만든 알고리즘을 말합니다. 이때의 Neural Networks가 무엇을 말하는 걸까요.
Neural Networks And Multi-Layer Perception
김성준 교수님이 소개해주신 NNs (Neural Networks) 정의가 너무나 인상깊었습니다.
- " NNs are Function Approximators that stack Affine Transformations followed by Nonlinear Transformation "
- '아핀 변환에 이은 비선형 변환' 들을 쌓는 함수 근사
참고로 아핀 변환이란 아핀 기하학적 성질(점, 직선, 평면)을 보존하는 선형 매핑 방법입니다.
직관적으로 이해하자면 선형 변환 후 시프팅 시킨 것이라 말할 수 있습니다.
시프팅(Translation)을 포함하기 때문에 선형 변환의 연장선상에 있는 개념이라고 할 수 있겠습니다.
( https://hooni-playground.com/1271/ )
초창기 딥러닝은 사람의 뇌를 모방하면서 출발하게 되었습니다. 가지 돌기를 통해 신호를 전달 받고, 축삭돌기를 통해 다른 뉴런에 신호를 전달하는 뉴런의 네트워크를 모방하였다고 하여 신경망이라고 하였습니다.
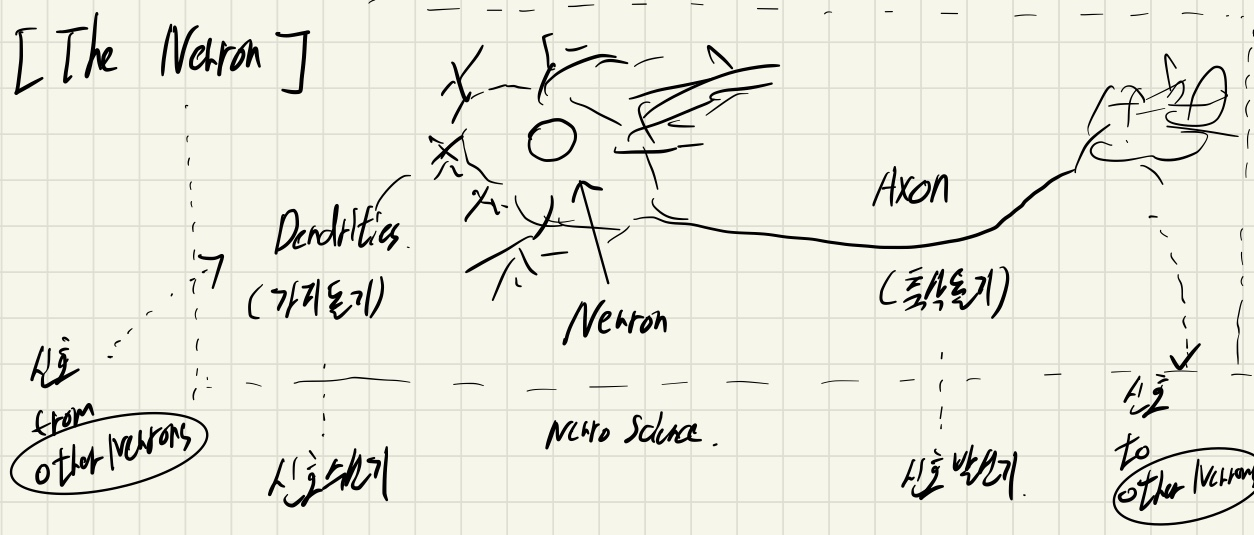
그러나 NNs를 단순히 '사람의 뇌를 모방한 것' 이라고 정의하기에는 NNs를 설명하기에 충분하지 않습니다.
실제로 NNs는 Feedforward Network과 Back Propagation의 수행에 용이한 수학적 모델이기 때문입니다.
여기서 질문이 있습니다.
- 아핀 변환에 이은 비선형 변환은 왜 하는 것이고,
- 왜 이들을 쌓는(stack) 것이며,
- 근사라는 표현은 왜 하는 것일까요?
- 그리고 Feedforward Network는 뭐고, Back Propagation는 무엇인가요?
Key Components In Deeplearning
딥러닝에는 아래의 4 가지 Key Components가 존재합니다.
- Data (Can Learn From)
데이터를 통해 우리는 어떠한 형태(Type)의 문제를 풀지(Approach) 알 수 있습니다. - Model (Transform The Data)
모델을 통해 데이터를 변환시킬 수 있습니다.(Data Transformation) - Loss Function (Quantifies Badness Of The Model)
Loss Function은 우리의 목적을 이룰 수 있도록 하는 근사 함수가 됩니다. - Alogorithm (Adjust Parameters To Minimize Loss)
여러 문제들을 해결하기 위한 일련의 절차 입니다.
ex) - 최적화 문제 (cetris paribus 하다면, 네트워크를 어떻게 줄일 수 있을지)
- 실환경에서의 동작 문제 (Eary Stopping, K-Fold, Ensemble, Drop out ....)
Loss Function을 설명할 때도 '근사' 라는 표현을 쓰네요?
데이터 샘플이 존재할 때, 우리는 주어진 데이터의 모집단의 분포를 알고 싶어 합니다.
그것이 지도학습을 하는 이유이겠죠. 따라서 참 값을 가지고 인공지능 모델을 훈련 시키고, 그에 따른 예측 값을 최대한 참 값에 근접하겠끔 추론하고자 합니다.
가령 MSE(Mean Squard Error)는 회귀 문제를 풀 때 있어서, Loss Function이 되는 대표적인 예시 입니다.
MSE가 커지면 커질수록 예측 값이 참 값으로부터 멀어진다는 것을 의미하기 때문에 MSE가 가장 작은 값을 갖도록 목적을 두는 것이 적합하다고 할 수 있겠죠.
그러나 여기서 한 가지 짚고 넘어가야할 점이 있습니다.
MSE는 어디까지나 우리의 목적에 대한 근사 함수이기 때문에 MSE가 준다는게 우리의 목적에 가까워졌다 라는 말과 동치는 아니라는 것 입니다.
이상치가 이슈가 되는 회귀 문제의 경우, 특정 이상치에 의해 MSE 값이 좌지우지 된다면 우리가 알고 싶어하는 general 한 case에 대한 예측이 불명확해집니다. 따라서 이상치의 영향을 덜 받는 절대값 (One-Norm Minimize) 또는 Robust Regression 과 같은 다른 Loss Function을 새로운 손실 함수로 제안할 수 있을 것입니다.
그러나 새롭게 제안된 함수가 실제 우리의 데이터에 맞는 손실 함수라고 100프로 확신할 수는 없을 것입니다. 또한 우리 데이터의 모집단에 맞는 손실 함수라고는 더욱이 확신할 수 없을 것입니다. 따라서 '근사' 입니다.
마찬가지로 NNs를 통해 우리는 예측 값이 실제 데이터의 모집단에 가까운 분포를 찾아낼 수 있어야 하는데, 우리가 구한 NNs가 정말로 이상적인 우리의 NNs라고 확신할 수 없기 때문에 '근사' 라는 표현을 쓰게되는 것 입니다.
NNs가 왜 작동을 잘 하는 것일까요?
Input Vector X가 있다고 합시다. 그리고 우리가 찾고자 하는 Output Vector Y가 있습니다.
NNs는 수학적 모델이고, NNs가 직면한 문제는 결국 X를 어떻게 잘 매핑해야 Y를 도출해낼 수 있을까 입니다.
X와 Y는 차원도 다를꺼고 그 값의 범위도 다를게 분명합니다. 가령 이미지를 가지고 강아지가 맞냐 틀리냐를 분류해내야하는 문제라고 가정한다면, X는 이미지 픽셀값이 되겠고, Y는 강아지면 1, 강아지가 아니면 0이 되는 값일 것입니다.
제 생각에 NNs에서 중요한 것은 NNs가 X값을 가지고 어디까지 '표현' 할 수 있을까 문제이지 않을까 싶습니다.
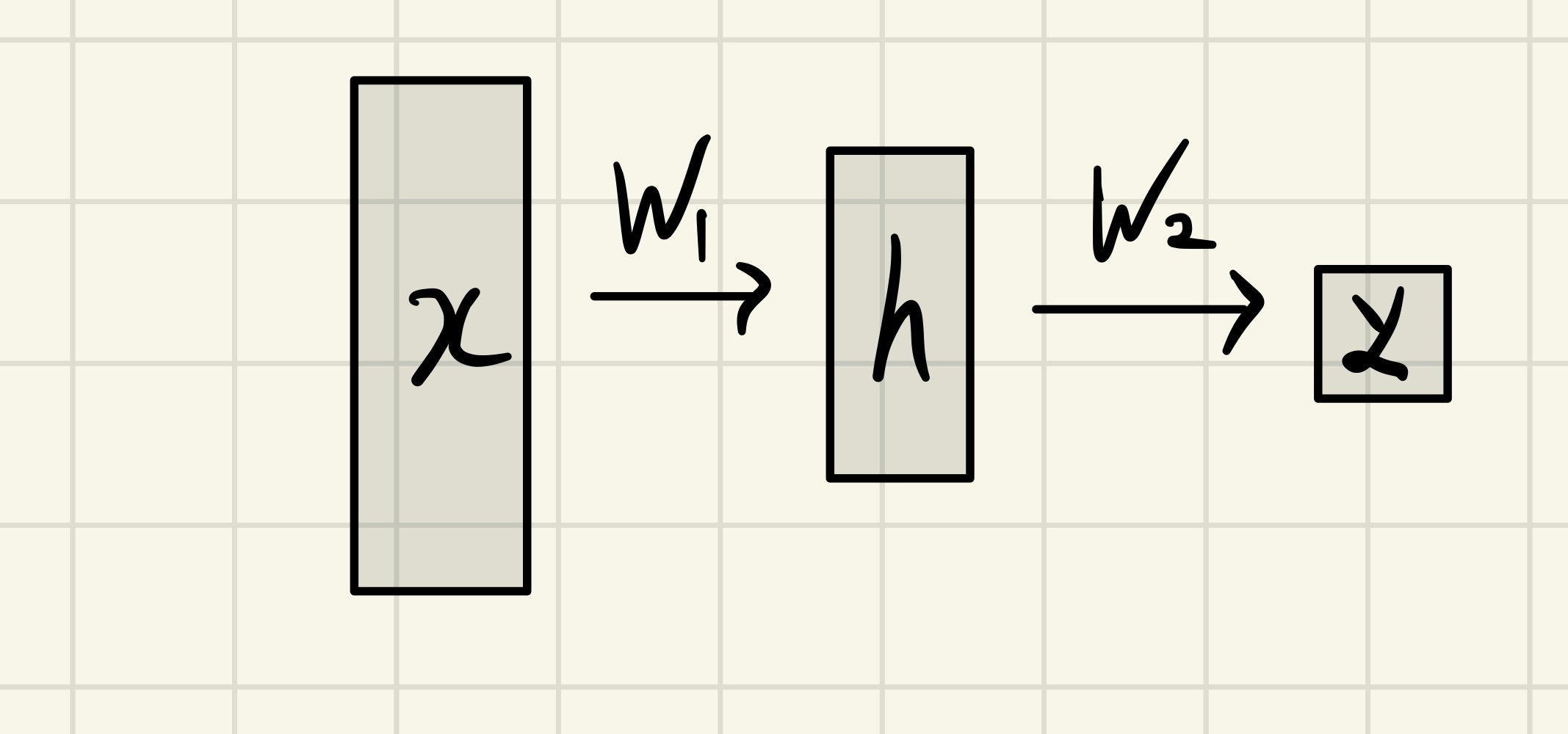
$$ Y = W_2^T \rho (W_1^TX) $$
- X 가 들어오게 되면 가중치(W)와 편향(B)가 연산됩니다. 이를 아핀 변환이라고 합니다.
일반적인 회귀함수를 떠올리면 좋을 것 같습니다. 수식은 편의상 Bias를 고려하지 않고 작성하도록 하겠습니다. - ρ 는 NonLinear Transformation인 활성화 함수 입니다.
아핀 변환이 이루어진 Input Vector는 활성화 함수를 통해 비선형 변환이 이루어지게 됩니다. - 이러한 과정을 한번 거치면 Input Vector는 h라는 값으로 변환하게 됩니다.
연산 과정에서 h 값이 어떤 값으로 변하는지는 우리가 알지 못하는 미지의 영역 (Black Box)이기 때문에, 이때의 레이어를 Hidden Layer 라고 합니다. 참고로 Input 단계의 레이어는 Input Layer 입니다.
이러한 과정을 통해 입력 값을 가지고 출력 값을 추론합니다. 이를 Feedforward Network 라고 합니다.
추론해낸 예측 값을 가지고 참 값과 비교하여 Loss 값을 계산해내고, 이를 가지고 가중치를 업데이트 합니다. 이를 Back Propagation 이라고 합니다.
추후 Back Propagation 에 대해 정리하도록 하겠습니다. 당장은 Back Propagation을 통해 각각의 가중치에 대해 순차적으로 업데이트 하는 것이 아니라 모든 가중치에 대해 동시에 업데이트 된다는것을 밝히고 지나가겠습니다.
이처럼 아핀 변환과 비선형 변환을 통해 X를 가지고 Y를 표현할 수 있습니다. 만약 이러한 과정을 N번 반복할 수 있다면 어떨까요? 모델은 참 값을 보다 잘 표현할 수 있게될 것입니다. 다른 말로 모델은 참 값에 대해 보다 잘 설명할 수 있게 됩니다.
만약 중간에 비선형 변환이 이루어지지 않는다면요?
만약 중간에 비선형 변환이 이루어지지 않았더라면 식은 아래와 같아집니다.
$$ Y = W_2^T(W_1^TX) = W^TX $$
결국 선형 변환을 N번을 하든, 한번을 한 것과 다를바가 없게 됩니다.
따라서 활성화 함수가 중요한 것입니다.
그럼 왜 작동이 잘 되나요?
"There's single Hidden Layer feedfoward network that approximates any measurable function to any desired degree of accuracy on some compact set K"
- Multilayer Feedforward Networks are Universal Approximators (1988) by Maxwell Stinchcombe, Halber White.
위 논문에 따르면 hidden layer가 단 하나만 존재하여도 그 어떠한 함수든 다 표현할 수 있을 정도로 표현력이 크다고 합니다. 저자는 이를 수식을 통해 증명해놓았습니다.
실제로 우리가 찾고자 하는 NNs를 찾는 것은 별개의 문제 이지만, NNs가 지닌 잠재성을 통해 왜 NNs가 작동이 잘 되는지를 충분히 유추해볼 수 있을 것 같습니다.
본 게시글은 Boostcourse 딥러닝 기초 다지기의 김성훈 교수님 강의를 듣고 작성한 글 입니다.
'DL > Basic' 카테고리의 다른 글
| Cross Entropy 맛보기 (0) | 2024.05.09 |
|---|---|
| Optimizer (1) | 2024.05.08 |
| 가중치 초기화 (Weight Initialization) (0) | 2024.05.07 |
| 1 x 1 Conv (1) | 2023.12.06 |
| Plateau Problem (0) | 2023.05.25 |
