딥러닝에서 Loss Function의 최솟값을 찾는 과정을 Optimization 이라고 합니다.
GD, SGD, mini-Batch GD 가 뭐에요?
$$ W_{t+1} = W_{t} - \eta g_t $$
함수의 기울기를 계산하여, 기울기의 반대방향으로 조금씩 이동하면서 최솟값을 찾아나가는 최적화 기법 입니다.
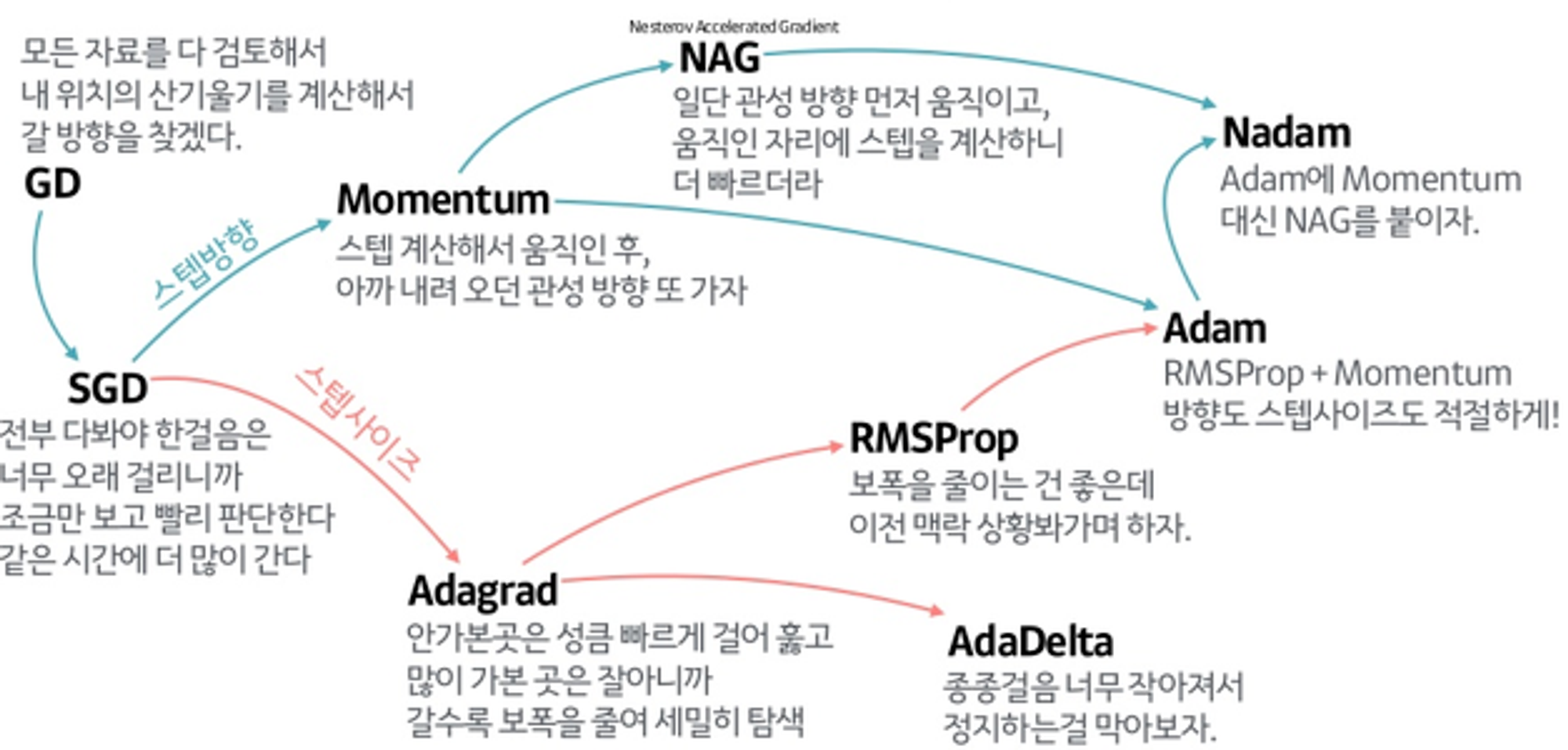
전체 학습 데이터를 대상으로 경사 (Gradient)를 계산하면 GD,
하나의 데이터를 골라, 경사를 계산하는 방법을 SGD,
GD와 SGD의 절충안으로, minibatch로 학습 데이터로 나누어 진행하는 방법을 mini-Batch GD 라고 합니다.
일반적으로 SGD 최적화를 수행했다고 하면, mini-Batch를 말한다고 보면 될 것 같습니다.
p.s.
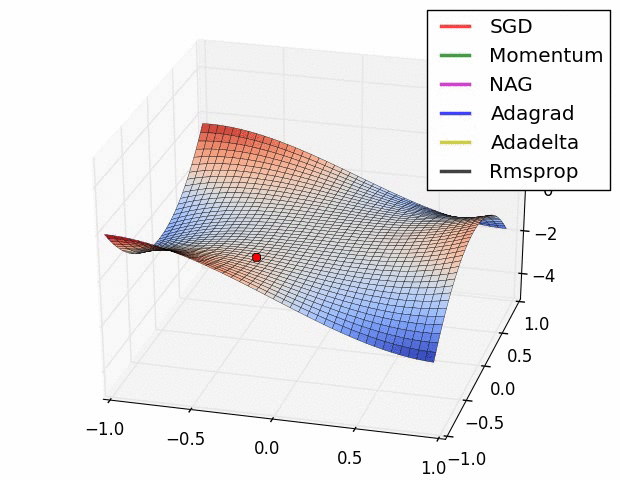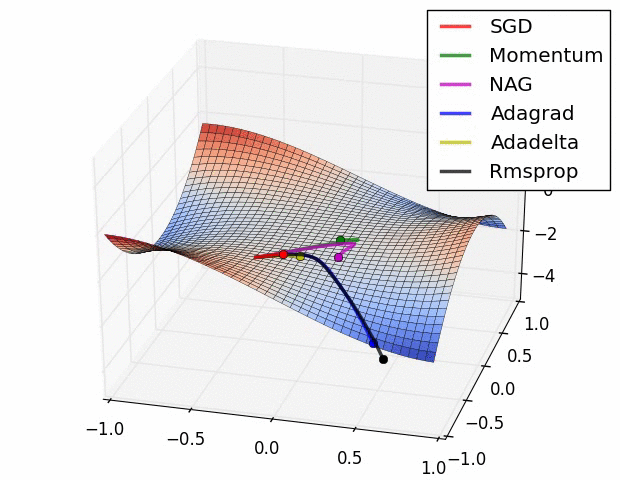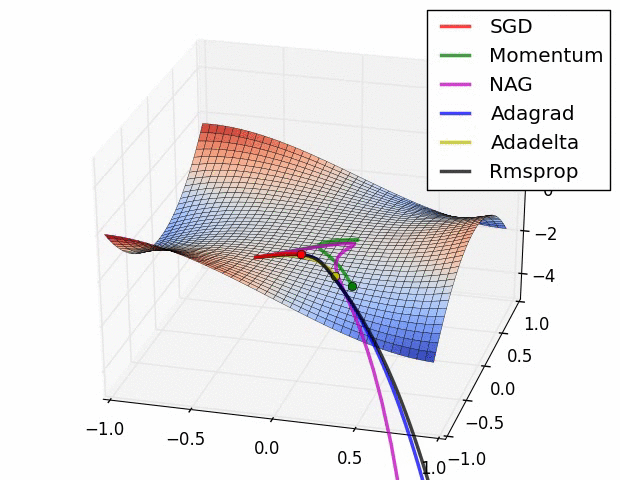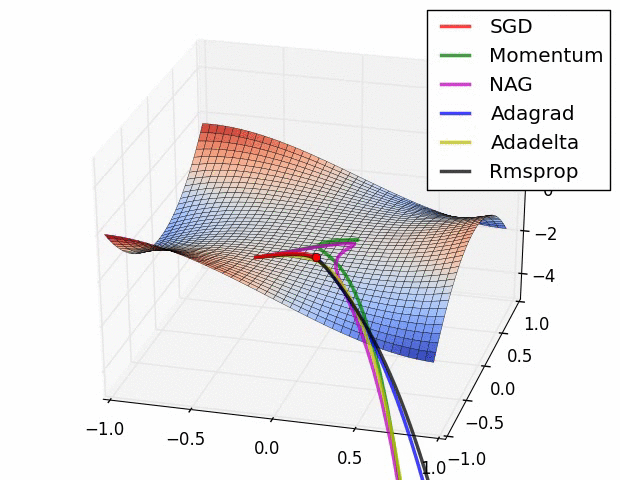
SGD를 수행하다보면, Iterate에 따른 비용 곡선이 상당히 진동하면서 가는것을 볼 수 있는데
매번 다른 경사 평균을 적용하여 최적화를 진행하기 때문에 그렇다고 보면 될 것 같습니다.
Momentum에 대해 설명해주세요.
$$ m^t=\gamma m^{t-1}-\eta g^t $$
$$ w^t = w^{t-1} + m^t $$
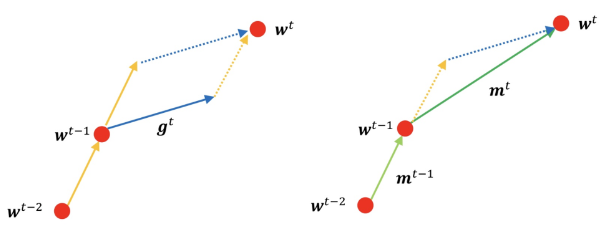
이전 경사, 현재의 경사를 모두 고려하여 가중치를 업데이트하는 기법 입니다.
모델을 더 빠르게 학습 시킬 수 있게 되었지만, 관성으로 인해 수렴하지 않고 발산할 수 있다는 단점이 있습니다.
NAG (Nesterov Accelerated Gradient) 에 대해 설명해주세요.
$$ a_{t+1} = \beta a_t + \nabla \mathcal{L}(w_t - \eta \beta \alpha_t) $$
$$ W_{t+1} = W_t - \eta a_{t+1} $$
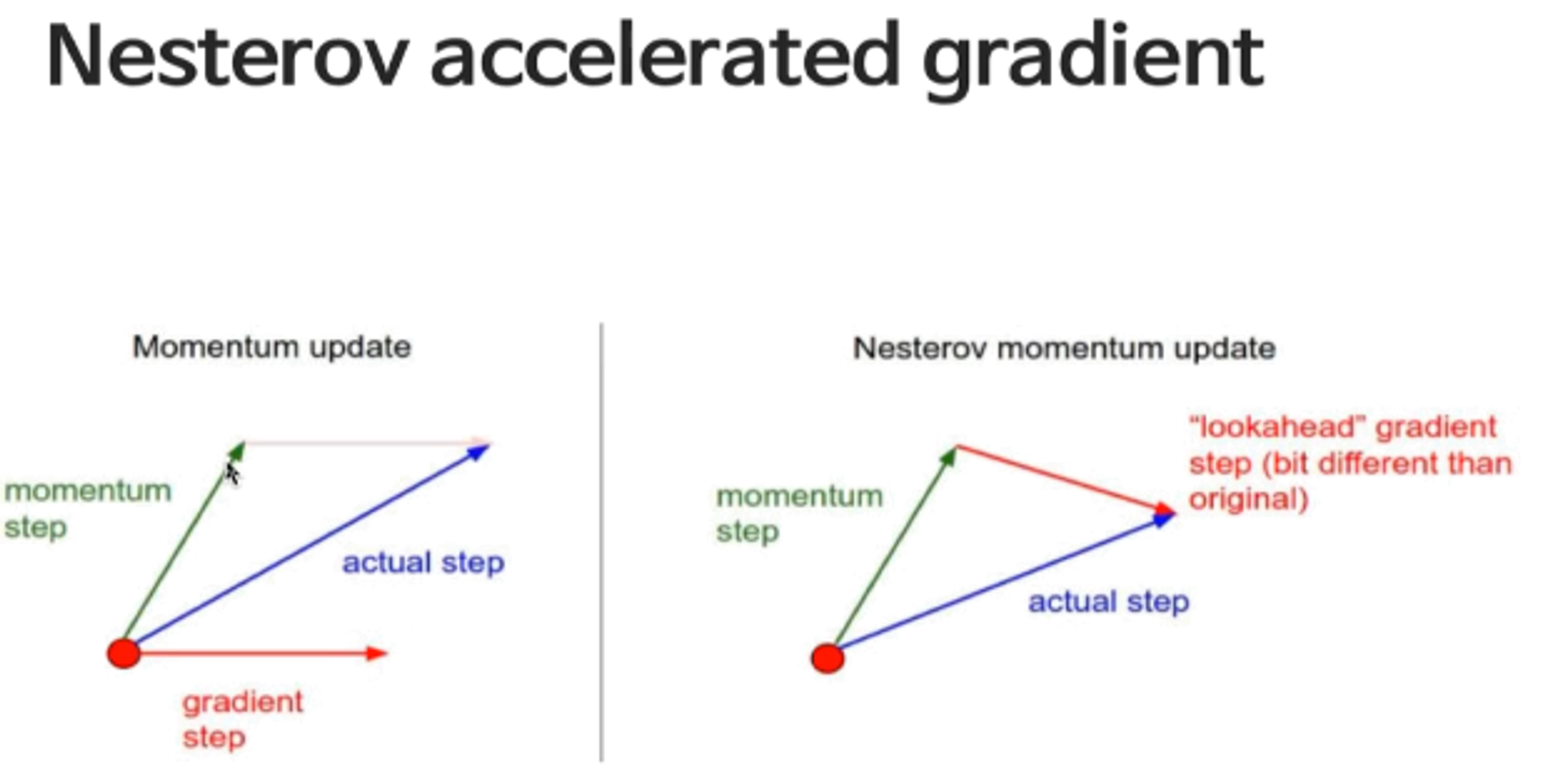
Momentum 기법을 사용했을 때, 관성으로 인해 최솟값 근방에 수렴하지 않고 발산한다는 단점을 극복하기 위한 기법 입니다.
우선 Momentum Step을 진행 후, 옮겨진 위치에서 Gradient를 구하여 Gradient Step을 갱신합니다.
이때의 Gradient를 Lookahead Gradient라고 합니다.
Momentum으로 나아간 스텝에 현재 경사에 따른 제동을 건다라고 생각하면 될 것 같습니다.
AdaGrad에 대해 설명해주세요.
$$ h_t = h_{t-1} + g_t^2 $$
$$ W_{t+1} = W_t - \frac {\eta} {\sqrt h} g_t $$
경사 제곱의 누적 값을 사용해 학습률을 조절하는 기법입니다.
경사에 의해 많이 업데이트 된 파라미터는 학습률이 감소하게 되고, 경사가 적게 업데이트 된 파라미터는 학습률이 증가하게 됩니다.
쌓아올린 경사가 크면 클수록, 해당 파라미터로 도달할 수 있는 최솟값에 임박해 있다고 생각하기 때문에 경사에 따른 Learning Rate를 줄이게 되는 것입니다.
첨언하자면, 관성으로인해 경사가 깊어지면 깊어질수록 Step Size가 점점 더 커지게 되는 Momentum과는 상반되는 기법이라고 볼 수 있을 것 같습니다.
RMSProp (Root Mean Square Propagation)에 대해 설명해주세요.
$$ h_t = \rho h_{t-1} + ( 1 - \rho )g_t^2 $$
$$ W_{t+1} = W_t - \frac {\eta} {\sqrt h} g_t $$
AdaGrad 기법을 그대로 사용하면, Gradient Square의 Monotonically Increasing Problem에 직면하게 됩니다.
따라서 학습이 거듭될수록 분모가 끝도 없이 커져, Step Size가 0으로 수렴하는 일이 발생하고 맙니다.
제프리 힌튼 교수님은 수업시간에, 이를 막기 위해 식에 지수 이동 평균(Exponential Moving Average) 개념을 도입해보았습니다.
과거 모든 경사 제곱을 단순히 누적하는 대신, 최근 경사 제곱에 더 많은 가중치를 두어, 과거의 데이터가 시간이 지남에 따라 점점 더 영향력이 감소하도록 하여 AdaGrad의 단점을 극복할 수 있었습니다.
* 식에서 로를 forgetting factor 라고도 하고, 감쇄율이라고 부르기도 한다고 합니다.
AdaDelta에 대해 설명해주세요.
$$ G_t = \gamma G_{t-1} + (1-\gamma)g_t^2 $$
$$ H_t = \gamma H_{t-1} + (1 - \gamma) (\Delta W_t^2) $$
$$ W_{t+1} = W_t - \frac{\sqrt {H_{t-1}+\epsilon}}{\sqrt {G_t + \epsilon _t} }g_t $$
학습률이 0으로 수렴해버리는 Adagrad의 단점을 보완하기 위한 기법 입니다.
RMSProp과 동일하게, Gradient Square을 사용한 연산에 지수 이동 평균을 도입하였습니다.
다만, Step Size에 대해 하이퍼파라미터를 정하는 대신, Step Size의 변화값의 제곱에 대한 지수 이동 평균을 사용을 사용하였습니다.
* Frist - Order Method 였던 SGD 에서와 달리 Second - Order Method를 사용한 최적화 기법이다.
Newton's method를 이용해 분자의 RMS (Root Mean Square), 분모의 RMS(Root Mean Square)값의 비율로 근사한 결과라고 한다.
Adam에 대해 설명해주세요.
$$ M_t = \beta_1 M_0 - (1 - \beta_1) g_t $$
$$ v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2 $$
$$ W_{t+1} = W_t - \frac {\eta}{\sqrt {v_t + \epsilon}}\frac{\sqrt {1-\beta_2^t}}{1-\beta_1^t}M_t $$
RMSProp 과 Momentum 기법이 합쳐져 만들어진 최적화 기법이다.
Momentum과 유사하게 기울기의 지수 평균에 따라 학습률을 높이며,
RMSProp과 유사하게 기울기의 제곱값들의 지수 평균에 따라 학습률을 낮춘다.
* 분모와 분자에 ( 1 - 베타 ) 와 같은 항이 들어가는 이유는 unbiased 하도록 만들어주기 위해 그렇다.
표본 분산을 구할 때 n - 1로 나누어주는 것과 같다고 생각하면 좋을 것 같다. ( 키워드 : 자유도, 불편 추정량 )
참고)
'DL > Basic' 카테고리의 다른 글
| CNN으로 MNIST 분류하기 (0) | 2024.07.13 |
|---|---|
| Cross Entropy 맛보기 (0) | 2024.05.09 |
| 가중치 초기화 (Weight Initialization) (0) | 2024.05.07 |
| 1 x 1 Conv (1) | 2023.12.06 |
| Plateau Problem (0) | 2023.05.25 |
딥러닝에서 Loss Function의 최솟값을 찾는 과정을 Optimization 이라고 합니다.


GD, SGD, mini-Batch GD 가 뭐에요?
Wt+1=Wt−ηgt
함수의 기울기를 계산하여, 기울기의 반대방향으로 조금씩 이동하면서 최솟값을 찾아나가는 최적화 기법 입니다.
전체 학습 데이터를 대상으로 경사 (Gradient)를 계산하면 GD,
하나의 데이터를 골라, 경사를 계산하는 방법을 SGD,
GD와 SGD의 절충안으로, minibatch로 학습 데이터로 나누어 진행하는 방법을 mini-Batch GD 라고 합니다.
일반적으로 SGD 최적화를 수행했다고 하면, mini-Batch를 말한다고 보면 될 것 같습니다.
p.s.
SGD를 수행하다보면, Iterate에 따른 비용 곡선이 상당히 진동하면서 가는것을 볼 수 있는데
매번 다른 경사 평균을 적용하여 최적화를 진행하기 때문에 그렇다고 보면 될 것 같습니다.
Momentum에 대해 설명해주세요.
mt=γmt−1−ηgt
wt=wt−1+mt

이전 경사, 현재의 경사를 모두 고려하여 가중치를 업데이트하는 기법 입니다.
모델을 더 빠르게 학습 시킬 수 있게 되었지만, 관성으로 인해 수렴하지 않고 발산할 수 있다는 단점이 있습니다.
NAG (Nesterov Accelerated Gradient) 에 대해 설명해주세요.
at+1=βat+∇L(wt−ηβαt)
Wt+1=Wt−ηat+1

Momentum 기법을 사용했을 때, 관성으로 인해 최솟값 근방에 수렴하지 않고 발산한다는 단점을 극복하기 위한 기법 입니다.
우선 Momentum Step을 진행 후, 옮겨진 위치에서 Gradient를 구하여 Gradient Step을 갱신합니다.
이때의 Gradient를 Lookahead Gradient라고 합니다.
Momentum으로 나아간 스텝에 현재 경사에 따른 제동을 건다라고 생각하면 될 것 같습니다.
AdaGrad에 대해 설명해주세요.
ht=ht−1+g2t
Wt+1=Wt−η√hgt
경사 제곱의 누적 값을 사용해 학습률을 조절하는 기법입니다.
경사에 의해 많이 업데이트 된 파라미터는 학습률이 감소하게 되고, 경사가 적게 업데이트 된 파라미터는 학습률이 증가하게 됩니다.
쌓아올린 경사가 크면 클수록, 해당 파라미터로 도달할 수 있는 최솟값에 임박해 있다고 생각하기 때문에 경사에 따른 Learning Rate를 줄이게 되는 것입니다.
첨언하자면, 관성으로인해 경사가 깊어지면 깊어질수록 Step Size가 점점 더 커지게 되는 Momentum과는 상반되는 기법이라고 볼 수 있을 것 같습니다.
RMSProp (Root Mean Square Propagation)에 대해 설명해주세요.
ht=ρht−1+(1−ρ)g2t
Wt+1=Wt−η√hgt
AdaGrad 기법을 그대로 사용하면, Gradient Square의 Monotonically Increasing Problem에 직면하게 됩니다.
따라서 학습이 거듭될수록 분모가 끝도 없이 커져, Step Size가 0으로 수렴하는 일이 발생하고 맙니다.
제프리 힌튼 교수님은 수업시간에, 이를 막기 위해 식에 지수 이동 평균(Exponential Moving Average) 개념을 도입해보았습니다.
과거 모든 경사 제곱을 단순히 누적하는 대신, 최근 경사 제곱에 더 많은 가중치를 두어, 과거의 데이터가 시간이 지남에 따라 점점 더 영향력이 감소하도록 하여 AdaGrad의 단점을 극복할 수 있었습니다.
* 식에서 로를 forgetting factor 라고도 하고, 감쇄율이라고 부르기도 한다고 합니다.
AdaDelta에 대해 설명해주세요.
Gt=γGt−1+(1−γ)g2t
Ht=γHt−1+(1−γ)(ΔW2t)
Wt+1=Wt−√Ht−1+ϵ√Gt+ϵtgt
학습률이 0으로 수렴해버리는 Adagrad의 단점을 보완하기 위한 기법 입니다.
RMSProp과 동일하게, Gradient Square을 사용한 연산에 지수 이동 평균을 도입하였습니다.
다만, Step Size에 대해 하이퍼파라미터를 정하는 대신, Step Size의 변화값의 제곱에 대한 지수 이동 평균을 사용을 사용하였습니다.
* Frist - Order Method 였던 SGD 에서와 달리 Second - Order Method를 사용한 최적화 기법이다.
Newton's method를 이용해 분자의 RMS (Root Mean Square), 분모의 RMS(Root Mean Square)값의 비율로 근사한 결과라고 한다.
Adam에 대해 설명해주세요.
Mt=β1M0−(1−β1)gt
vt=β2vt−1+(1−β2)g2t
Wt+1=Wt−η√vt+ϵ√1−βt21−βt1Mt
RMSProp 과 Momentum 기법이 합쳐져 만들어진 최적화 기법이다.
Momentum과 유사하게 기울기의 지수 평균에 따라 학습률을 높이며,
RMSProp과 유사하게 기울기의 제곱값들의 지수 평균에 따라 학습률을 낮춘다.
* 분모와 분자에 ( 1 - 베타 ) 와 같은 항이 들어가는 이유는 unbiased 하도록 만들어주기 위해 그렇다.
표본 분산을 구할 때 n - 1로 나누어주는 것과 같다고 생각하면 좋을 것 같다. ( 키워드 : 자유도, 불편 추정량 )
참고)
'DL > Basic' 카테고리의 다른 글
| CNN으로 MNIST 분류하기 (0) | 2024.07.13 |
|---|---|
| Cross Entropy 맛보기 (0) | 2024.05.09 |
| 가중치 초기화 (Weight Initialization) (0) | 2024.05.07 |
| 1 x 1 Conv (1) | 2023.12.06 |
| Plateau Problem (0) | 2023.05.25 |
