Vaswani, Ashish, et al. "Attention is all you need." Proceedings of the Advances in Neural Information Processing Systems. 2017.
소개
Seq2Seq 가 갖는 한계
- 순차적 계산, 병목 현상, 정보 손실

Idea
- 하나의 문맥 벡터가 시퀀스의 모든 정보를 가지고 있어야해서 성능이 저하된다면,
매번 모든 시퀀스에서의 출력 전부를 입력으로 받으면 어떨까? - 그리고 행렬곱을 이용해 전체 시퀀스를 한번에 연산하면 되지 않을까?
=> Scaled-Dot Product Attention
Abstract

- 배경
- 전통적으로 시퀀스 변환 모델은 인코더와 디코더로 구성된 복잡한 순환 신경망 또는 컨볼루션 신경망을 기반으로 하였다.
- 제안된 모델
- 인코더와 디코더 모두 전적으로 Attention 매커니즘에 기반한 모델을 소개
- 전통 모델과 비교한 결과 병렬 처리가 더 우수하고, 훈련 속도가 더 빠릅니다.
- WMT 2014 English-to-German translation 에서 28.4 BLEU를 달성, 기존 최고 결과보다 2 BLEU 향상
- WMT 2014 English-to-France translation 에서 8개의 GPUs로 3.5일간 학습, 41.0 BLEU를 달성하였습니다.
Introduction
- 순차적 계산의 근본적인 제약 w.r.t. Recurrent Models.
- 기존의 S.O.A.
- 순환 신경망( 특히 Long Short-Term Memory과 Gated Recurrent Neural Networks )은 그동안 Language Modeling and Machine Translation 에서 S.O.A. 로 활약하며 순환 언어 모델과 인코더-디코터 아키텍처의 한계를 넓히기 위해 이어져 왔습니다.
- 순차적인 특성
- 입력과 출력 시퀀스의 기호 위치에 따라 계산을 분해
- 계산 시간에 따라 위치를 정렬하여, 이전 hidden state ht-1 와 위치 t의 입력을 기반으로 ht를 생성
- 한계
- 병렬 훈련이 불가능
- 메모리 제약으로 인한 시퀀스 길이(배치) 제한
- 개선 노력
- Factorization tricks, Conditional Computation
- Computation 성능을 향상시킬 수는 있었지만 순차적 계산의 근본적인 한계를 극복할 수는 없었음.
- 기존의 S.O.A.
- Attention Mechanisms
- 입력 또는 출력 시퀀스 거리와 관계 없이 모델링
- Recurrent Model이 갖는 한계를 극복하기 위해 주로 같이 사용되어옴.

- Recurrent를 배제한 Transformer
- 입력과 출력 간의 전역적인 종속성을 Attention Mechanisms에 의존
- 훨씬 더 많은 병렬화
- 8개의 P100 GPU에서 12시간만 훈련하면 번역 품질에서 최첨단 수준에 도달할 수 있다.
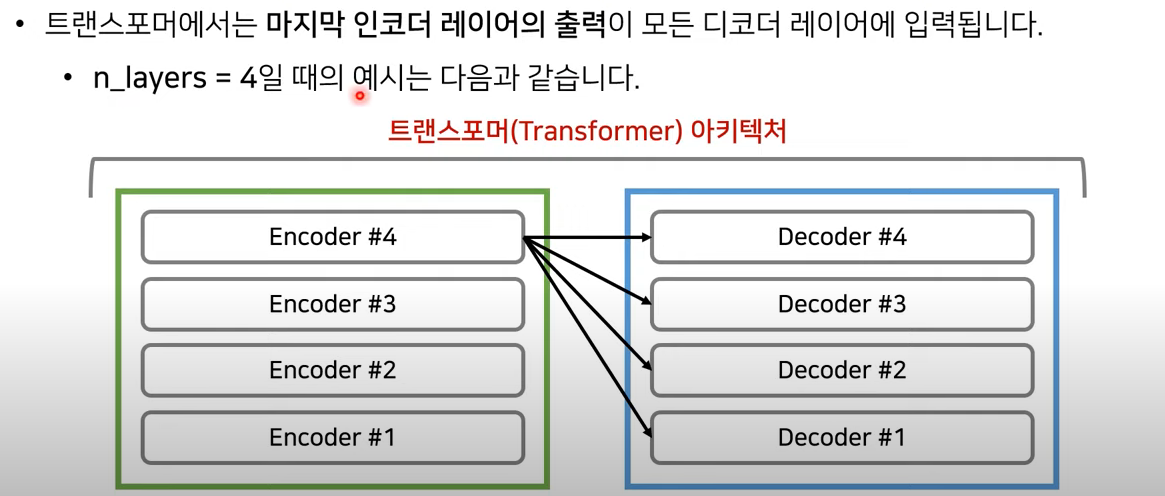
Architectures

Encoder
Embedding
네트워크에 넣기 전, 입력값들을 Embedding 형태로 표현한다. (적은 차원의 continuous한 값)
각각의 단어들에 대해서, 정보를 포함하고 있는 embedding dimension을 정하여 구할 수 있다.
( 본 논문에서는 512개 임베딩 채널을 구성 )
Positional Encoding
RNN을 사용하지 않으려면 위치 정보를 포함하는 임베딩이 필요하다.
이를 위해 트랜스포머에서는 Positional Encoding을 사용한다.
본 논문에서는 sin cos 과 같은 주기 함수를 사용하고, 각각의 데이타에 대해 가령 (0,3) 이면 0번째 시퀀스의 3번째 단어 와 같이 결과가 나오게 된다. 나온 결과에 대해 element wise sum 한다.
고정된 함수를 사용할 수도 있지만, Positional Encoding 에 대한 layer를 추가하여 아예 Position에 대한 학습을 또한 진행할 수 있고 실제로 최신 논문에서는 이러한 방식을 사용한다고 한다.
그러나 유의미한 성능차이가 크지 않다고 한다.
Scaled Dot-Product Attention
- 3 개의 행렬 Q, K, V
- Q ( Queries ) : 비교하고자 하는 시퀀스로, 키 K 와 유사도를 측정
- K ( Keys ) : 비교 대상이 되는 시퀀스로, 쿼리 Q 와 유사도를 측정
- V ( Values ) : QK의 가중치가 곱해지는 행렬
- 예시
- I Love You 에 대해 Self Attention을 적용시킨다고 가정해보자.
- I 가 0 번째 Q라면
- I, Love, You 가 이에 대한 K 값이 된다.

$$ Attention(Q,K,V) = softmax({QK^T \over \sqrt d_k})V $$
- MatMul
- dot product를 통해 쿼리 Q와 키 K 간의 유사도를 분석한다.
- Scale
- Q*K는 차원 d의 루트를 통해 scaled
- Softmax
- Softmax를 통해 각 유사도에 대한 가중치 값을 구할 수 있다.
- MatMul
- 구한 가중치를 value 값 V에 반영함으로써 모든 쿼리에 대한 어텐션을 얻을 수 있다.
- Additive Attention와 Dot-Product Attention
일반적으로 Attention 함수에는 Additive Attention과 Dot-Product Attention가 있는데 Transformer에서는 Dot-Product Attention이 쓰였다. 이론적으로는 유사하지만 매우 최적화된 행렬 곱셈 코드를 사용한 Dot-Product가 훨씬 빠르고 Space-Efficient 하다는 강점이 있다.
d_k가 작을 때 두 매커니즘의 성능은 유사하지만, d_k 값이 클 때는 Additive Attention이 보다 우수한 성능을 보인다. 이는 softmax 함수가 기울기를 극도로 작게 scale 하기 때문이라고 추측되며 따라서 Scale 단계를 통해 차원 d의 루트를 곱하였다. 그럼으로써 d_k 값이 클 때 발생할 수 있는 Gradient Vanishing 문제를 해결할 수 있다고 한다.

NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE 2015
어텐션은 쿼리와 키의 Heatmap을 생성하는 것과 같다.
전체 시퀀스를 (q, k)로 살펴보기 때문에, 단어가 문장에서 등장하는 순서에 관계없이 유사도를 계산할 수 있다.
위의 예는 어순이 다른 영어와 프랑스어를 가지고 구한 유사도를 표현한 그래프이다.
Multi-Head Attention

- Multi-Head Attention?
d 차원의 Q, K, V 를 단일 어텐션 함수에 한번에 적용하는 대신,
- Q, K, V 각각에 대해 서로 다르게 학습된 선형 변환을 적용시킨 뒤,
- 입력값에 대해 h번 어텐션을 수행한 후,
- 결과를 결합(concat) 하여 최종적으로 하나의 행렬을 만드는 것을 뜻한다.
이때 여러번의 어텐션은 병렬 연산으로 진행할 수 있고,
매번 학습할 때마다 다른 가중치를 가지므로 시퀀스 간의 다양한 관계에 대하여 학습할 수 있다.
- 수식
$$ MultiHead(Q,K,V) = Concat(head_1, ..., head_h)W^O $$
$$ \text{ where } head_i = Attention(QW_i^Q, KW_i^K, VW_i^V)$$
- "Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this."
- Q, K, V 를 서로 다른 하위 공간으로 선형 변환하여 다른 종류의 정보를 학습한다.
- 병렬로 입력 시퀀스의 다른 부분에 주의를 기울이면 모델은 데이터의 더 다양한 표현을 학습하고 여러 관점에서 정보를 효과적으로 처리할 수 있다.
- 단일 어텐션 헤드를 사용하게 되면 모델이 서로 다른 표현 하위 공간을 동시에 주의할 수 없고, 따라서 모든 위치에 걸친 어텐션 가중치를 평균화하게 되면서 희석된 표현을 만들어내게 된다.
- 가중치의 평균은 모델의 특정 부분을 집중하거나 세밀한 패턴을 잡아내는 능력을 제한하게 된다.
잔여 학습 (Residual Learning)

ResNet에서 사용되는 기법 ( Residual Connection )
초기 학습 성능을 높혀, 글로벌 미니멈을 보다 용이하게 찾게 해주는 테크닉
정규화 과정의 반복
- 어텐션과 정규화 과정을 반복합니다.
- 각각의 레이어는 서로 다른 파라미터를 파라미터를 갖습니다.
- 입력 Dimension과 출력 Dimension이 같습니다.
Decoder
Why Self-Attention
각각의 단어들이 서로가 서로에게 어떠한 가중치를 가지는지를 구하도록 만들어서 출력되고 있는 문장의 전반적인 관계와 표현을 학습되도록 만든다.
정리
https://jalammar.github.io/images/attention_process.mp4


https://ai.googleblog.com/2017/08/transformer-novel-neural-network.html
Implementation
Experiments
Conclusion
추가로 언급할만한 내용
* 풀잎스쿨 딥러닝 논문 요약 및 구현 스터디에서 진행한 내용 입니다.
* 샤라웃 동빈나! (https://www.youtube.com/watch?v=AA621UofTUA)
* 부스트코스 동기, 일레븐님 블로그 https://nearnear.github.io/AI/Text/transformer/?category=all#blog
* 어텐션 매커니즘을 이해하는데 도움이 됐던 https://glee1228.tistory.com/3
'DL' 카테고리의 다른 글
| [YOLO; You Only Look Once] Unified, Real-Time Object Detection (0) | 2023.06.29 |
|---|---|
| 순환 신경망 실습 (0) | 2023.06.25 |
| [ResNet] Deep Residual Learning for Image Recognition (0) | 2023.06.22 |
| Docker를 통한 Jupyter Notebook 접속 (0) | 2023.05.04 |
| 학습환경 세팅 ( Docker ) (0) | 2023.05.04 |
