He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. "Deep Residual Learning for Image Recognition." IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016.
선행 지식 ) CNN 모델에 대한 기본적인 개념
소개
깊은 네트워크를 학습시키기 위한 방법, 잔여 학습(Residual Learning)을 제안
아래의 그래프는 Train에 대한 Error, OverFitting 의 문제가 아님을 알 수 있다.
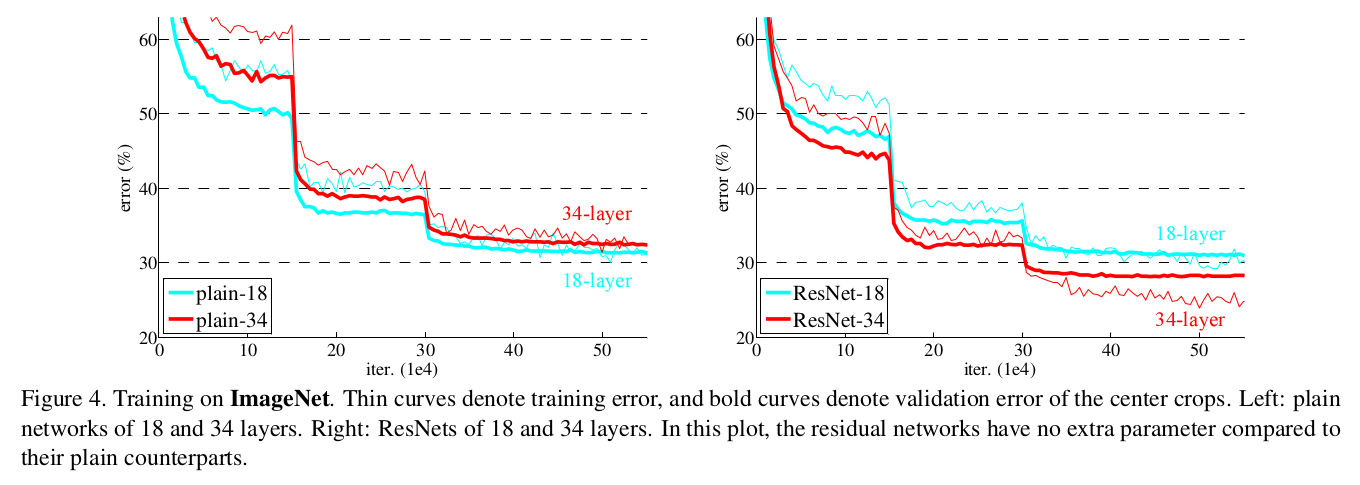
더 깊은 레이어가 더 좋은 성능을 보인다는 일반적인 양상을 유지할 수 있도록 보여주었다는 점이 본 논문이 기여하는 바 이다.
* 일반적인 양상
AlexNet(8층) → VGGNet(19층) → GoogLeNet(22층) 신경망 층수가 많을 수록 이미지에서 좋은 특징 추출이 가능해짐.
Abstract

- 배경
- Neural Networks 가 깊어질수록 오히려 Train이 어려워지는 문제
- 해결
- Residual Learning Framework
- Easy Optimize, Accuracy increased by Deeper Depth
- VGG nets 보다 8배 깊은 레이어 (152 레이어) & 낮은 Complexity
- ResNet의 앙상블 모델을 통해 3.57% error을 거둠으로써 ILSVRC2015 분류 대회에서 1등
- Depth 의 중요성
- 단순히 분류에서 뿐만 아니라, ImageNet Localization, COCO Object Detection, COCO Segmentation 에서 Foundation 모델로 사용했을 때, 1등을 할 정도의 성능을 보임
- Residual Learning Framework
Introduction
- Deep Convolutional Neural Networks
- Deep CNN은 이미지 분류에 있어서 돌파구와도 같은 혁신을 가져왔습니다.
- 단일한 엔드 투 엔드 다중 계층 구조로, Low / Mid / High level의 featrues의 특징 및 분류기를 자연스럽게 통합한다.
- Feature의 "level"은 계층을 얼마나 쌓느냐에 결정되는데, 여러 개의 레이어로 구성된 분류기를 거치며 점진적으로 더 복잡하고 추상화된 특징을 학습하기 때문에 Feature의 "level"은 입력 데이터로부터 얼마나 고수준의 표현을 학습하여 복잡한 패턴 및 특징을 인식하고 분류할 수 있을지와 연관되어 있다고 말할 수 있겠다.
- Is Learning Better Networks as Easy as Stacking more Layers?
- Vaninshing/Exploding Gradients Problem.
- 해당 문제를 해결하기 위해 제안된 방법들이 있습니다.
- Normalized Initialization ( 적절히 초기화를 해보자. )
"Delving Deep into Rectifiers", Kaiming He, 2015 - Intermediate Normalization Layers
- Normalized Initialization ( 적절히 초기화를 해보자. )
- When deeper networks are able to start converging, A Degradation Problem has been exposed.
Not Caused by Overfitting.- 어느 순간 정확도가 더 이상 증가하지 않고 오히려 감소하는 현상
- 층을 높이는 것은 Training Error을 높이게 됨 ( 위의 소개에서 살펴본 그래프 참조 )
- 그럼 Identitiy Mapping 을 깊게 쌓으면 되지 않을까...? Identitiy Mapping 이기 때문에 깊게 쌓아봤자 연산력이 증가하지도 않을꺼고, Training Error가 증가하는 일 또한 없을 테니깐.... →본 논문의 아이디어 출발점 이라고 볼 수 있겠다.
Deep Residual Learning
- 잔여 블록 (Residual Block)을 이용해 네트워크의 최적화(Optimization) 난이도를 낮춘다.
- 내재한 mapping인 H(x)를 곧바로 학습하는 것은 어려우므로 대신 F(x) = H(x) - x 를 학습한다.
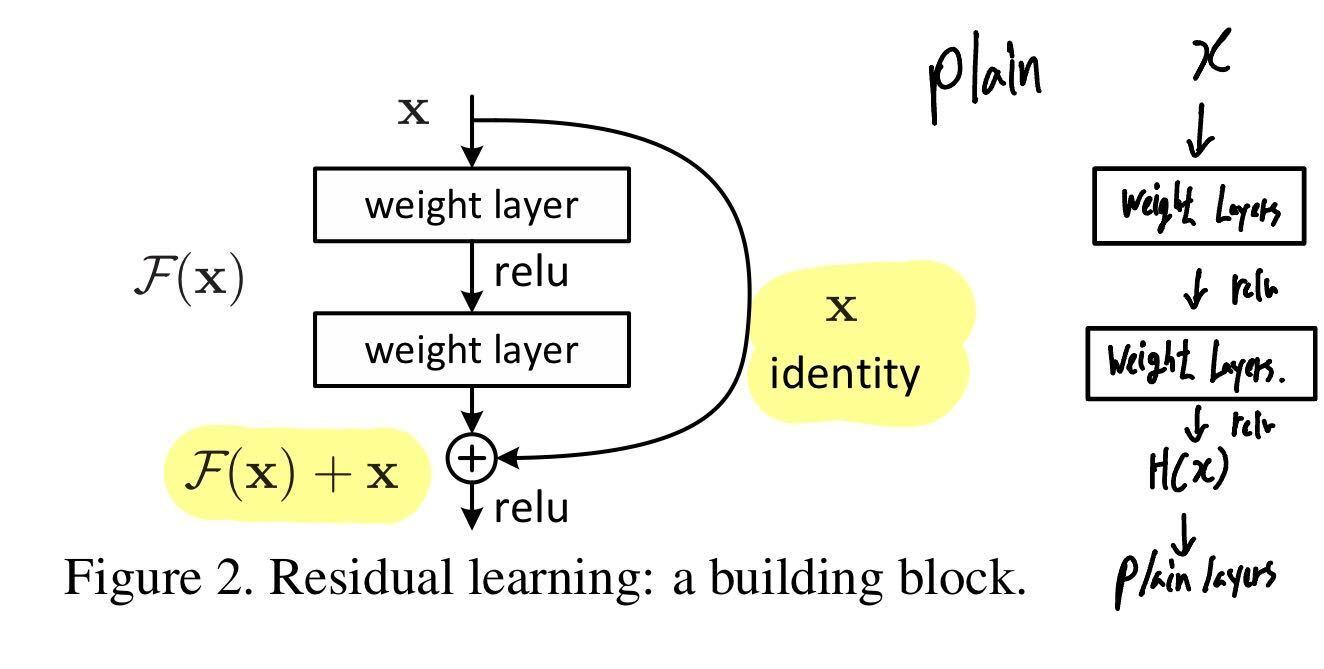
앞서 학습된 정보인 x identity를 그대로 가져오고, 추가적으로 잔여한 정보인 F(x)를 더해준다.
- 위 이미지에서 정의한 F
$$ F = W_2\sigma (W_1x)$$
- In general
$$ y = F(x,{W_i}) + W_sx $$
F에 대한 연산을 multiple convolutional layers 라고 정의할 수 있고, x에 대한 연산을 shorcut 이라 정의할 수 있다.
입력 값의 Dimension과 출력 값의 Dimension이 동일하다면, Identity Mapping을 수행할 수 있고, 만약 다르다면 위 식에서와 같이 Linear하게 Projection 하여 연산할 수 있다. (W_s)
극단적으로, 우리가 목표로 하는 H(x) 가 가령 x 라면, 잔차가 0임을 의미하므로 난이도가 더 쉬울 수 있다는 것을 의미한다고 한다.
- 스콘이 이해한 바
직관적으로 이해하기로는, H(x)가 실제로 어떠한 함수인지 모르는 상황에서 우리는 점진적으로 H(x)를 찾아나가고 있고( 여러 개의 비선형 레이어를 이용하여 ), 단순히 H(x)가 대강 x일 것이다 라고 짐작하고 시작하는 것 만으로도 최적화 난이도를 상당히 낮출 수 있다는 것으로 이해된다.
Shortcut Connection ( Identitiy Block, Skip Connection) 을 추가한다고 해서 파라미터가 추가되지도 않고 복잡도가 더 증가하지 않으며, 구현에 용이하고 Train Error가 증가하지도 않을 것이라는 점에서 매우 유용한 접근법 이었고, 검증 결과 실제로 탁월하더라.
p.s. 만약 x라고 Identity Mapping을 하지 않는다면, 사실상 0 이라고 Zero Mapping을 하는 것이기 때문에, 당연히 H(x)는 0이기 보다 x에 가까울 가능성을 높게 보는게 맞는 것일 수 있다. (논문에 나온 내용)
다시 말해, 0에서 H(x)를 찾아가는 것 보다 x에서 H(x)를 찾아가는게 더 쉽다.
- 풀잎 스쿨에서 스터디원 분이 답변해주신 질의응답 내용

특정 상수로 f(x)를 수렴시킨다는게 보다 쉽게 Optimizer 될 수 있는 명료한 목표가 된다는 점에서 매우 인상 깊었던 질의응답이었습니다.
물론 H(x)가 실제로 x가 될 수는 없겠지만, F(x)를 잔차로 취급한다는게 어떻게 보면 H(x)를 x로 수렴시킨다는 의미가 될수도 있을 것 같습니다. 실제로 x는 CNN의 Non-linear한 과정을 통해 훈련 되어 나온 값이기 때문에 실제로 H(x)와 유사할 가능성이 높다고도 할 수 있을 것 같습니다.
p.s. 논문에 따르면 Experiment 결과 Residual Function이 실제로 Small Response를 보여주었다고 하는 걸 보니, H(x)를 x라고 추측하는게 정말로 탁월한 선택이었네요.
- Residual 의 효과에 대한 또다른 질의응답

Vanishing Gradient가 역전파 과정에서 h'(x)가 너무나도 0에 가까운 값이 되기 때문에 발생하는 문제라고 한다면, 실제로 1을 더해줌으로써 0에 가까운 값이 되지 않도록 하는 역할을 수행한다고 볼 수 있을 것 같습니다.
해당 내용을 보면서 LSTM의 Cell State가 생각이 났어요.
- 주의할 점
- F 를 사용할 때, Single Layer로 사용하게 되면 하나의 Linear Layer가 사용된 것과 마찬가지이기 때문에 사용하는 의미가 없게 된다. 따라서 여러개의 레이어를 중첩한 값을 통해 유의미한 F 값으로 만들어주어야 한다.
Architectures
VGG 에서 제안된 기법을 그대로 사용하여 Plain Network 구성
- 3 x 3 filters following 2 simple desigin rules
- output feature map size가 같도록 해주기 위해, 같은 갯수의 filter를 사용
- feature map 사이즈가 절반으로 줄어들게 되면, 필터의 갯수를 두배로 늘림 ( time complexity 보존 )
- 별도의 Pooling layer을 사용하지 않고, Convolutional layers에서 stride 값을 2로 설정하고 down sampling을 진행.
- 결과적으로 1000개의 클래스로 분류할 수 있도록 마지막에 softmax를 사용한 fully connected layer로 구성
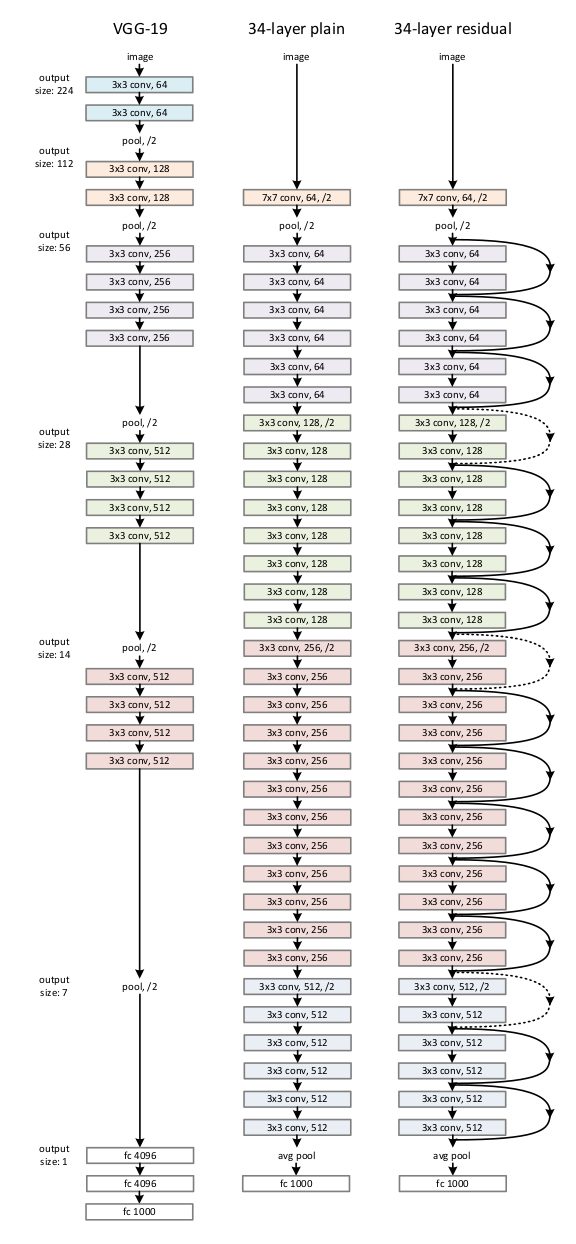
* 위 그래프의 점선 Short Connection은 Dimension 의 일치를 맞춰주기 위한 테크닉이 적용된 구간 opt1, opt2
opt1) Identity Mapping with Extra zero entries padded for increasing dimensions
opt2) Projection 연산을 허용한 Shorcut Connection
Projection을 늘 적용시킬 경우 성능 개선이 높았지만, 유별한 차이는 아니라고 한다.
* FLOPs : 계산 복잡도를 나타내기 위한 척도
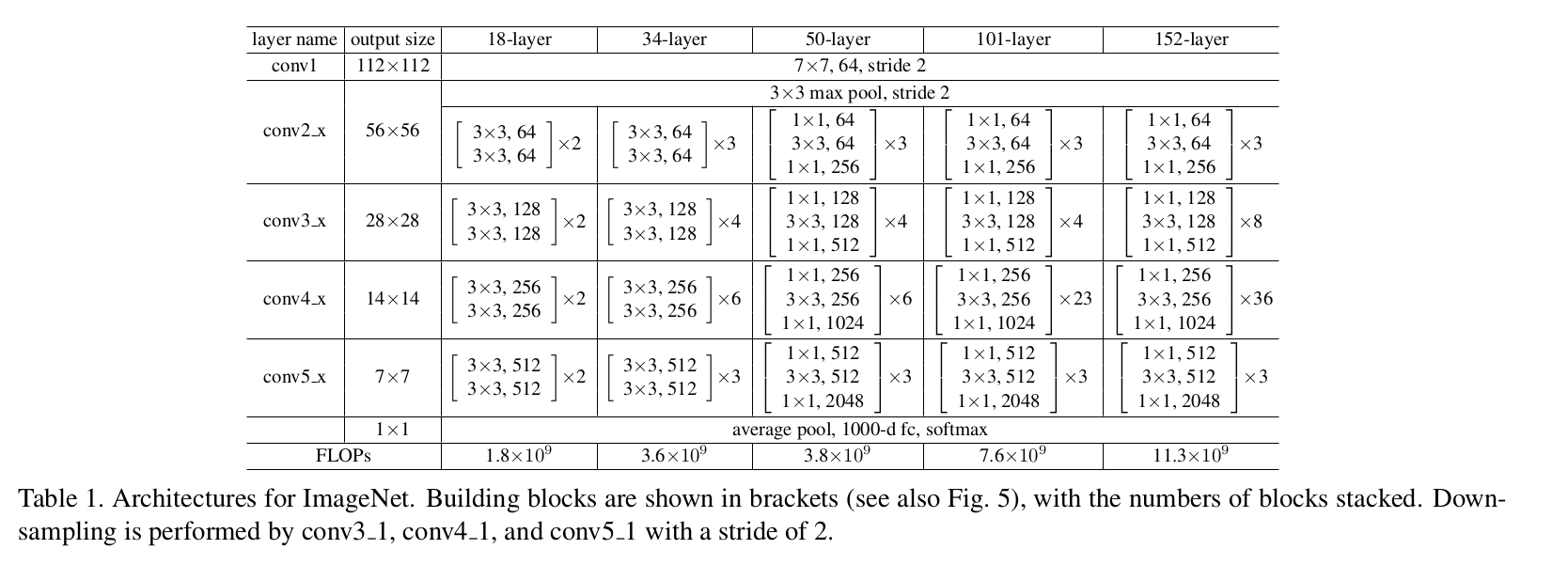
Implementation
Augmentation
- [256, 480] 범위 random resize
- 224 * 224 random crop + Horizontal flip
- Standard Color Augumentation
- 매 Convolution 연산 마다 Batch Normalization
- Initialization
- SGD optimizer
- 256 mini batch
- Learning Rate 0.1에서 시작, 정체 시 0.1배
- 60 * 104 iteration ( 60만 회 )
- 0.0001 Weight decay, 0.9 Momentum
- Dropout 사용 x
- 10 Cross Validation
- {224, 256, 384, 480, 640} 중 하나로 resize하고 평균 score 산출
Experiments
- ImageNet 2012 Classification dataset ( 1000 classes )
- 1.28 bil train data, 50k validation data, 100k test data
- Plain과 잔여블록을 사용한 모델 (ResNet) 간의 비교

- 앙상블을 적용하여 성능을 높힌 결과, 이전의 S.O.A에 비해 훨씬 높은 결과를 보였다.
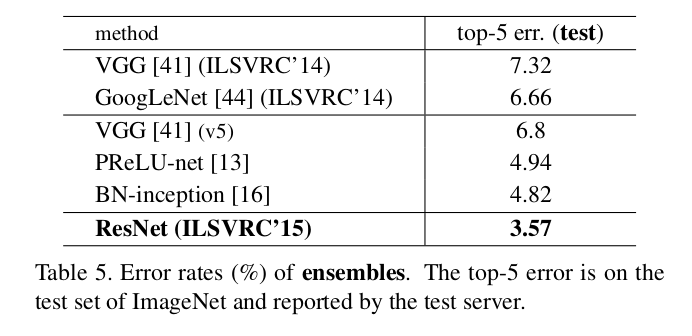
- 앙상블을 사용하지 않고 Single 모델을 사용했을 때 보여준 성능
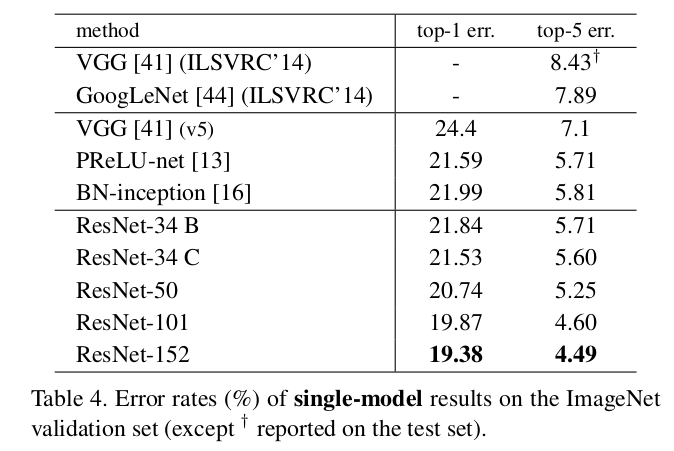
Conclusion
ResNet과 다른 Plain Network를 비교했을 때, 깊은 레이어가 얕은 레이어보다 더 잘 동작하는것을 보여주고 있으며, train error 또한 줄어들고, 일반화 성능 또한 높았다. 결과적으로 초기 단계에서 더 빨리 수렴할 수 있도록 만들어줌으로써 Optimization 자체를 더 쉽게 만들어준다는 점이 장점이라고 할 수 있겠다.
추가로 언급할만한 내용
Degradation Problem
Forward와 Backword Signal 을 확인한 결과 점진적으로 vanish 되는 현상은 발견되지 않았기 때문에 본 논문에서는 Degradation Problem에 대해 Vanishing Gradient Problem으로 보지 않음.
저자의 추측에 따르면, Exponentially Low Convergence Rates 에 의한 문제에 의한 것 같다고 함.
* Convergence Rates : 최적화 기법에서 등장하는 개념으로, 수렴을 위해 필요한 epoch이나 수렴 난이도를 언급하고자 할 때 사용하는 척도.
Bottle Neck Design
- 복잡도를 증가시키지 않기 위해 사용되는 디자인
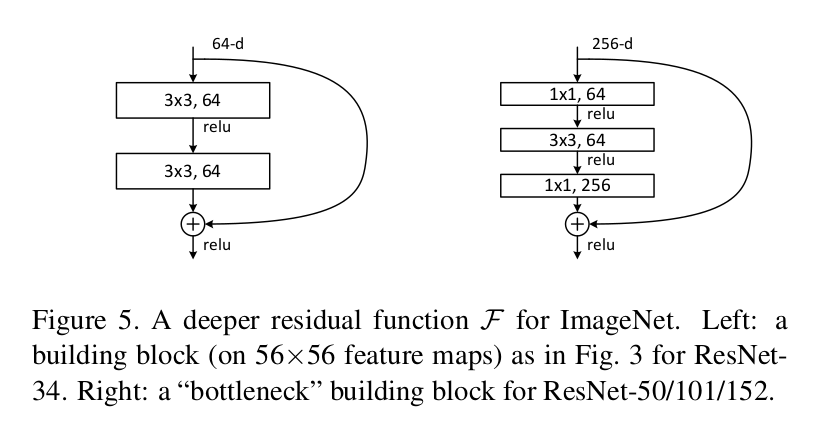
Identity Shorcut은 Parameter 자체가 존재하지 않기 때문에 Bottle Neck Architecture에 대해서 보다 효과적으로 파라미터의 수를 줄이는데 기여할 수 있다고 한다.
만약 Identity Short Cut이 Bottle Neck 구조가 아니라 Projection으로 대체된다면, time complexity와 model size가 모두 2배가 되기 때문에 보다 효율적인 모델을 만들기 위해서는 Bottle Neck 구조가 필수적이라고 한다.
관련 참고 링크 ) https://coding-yoon.tistory.com/116?category=825914
실제로 위 그림을 가지고 파라미터의 갯수를 계산해보자면,
| Not Bottle Neck Design | 1st layer : 3 x 3 x 64 x 64 = 36864 2st layer : 3 x 3 x 64 x 64 = 36864 total parameter : 74k |
| Bottle Neck Desigin | 1st layer : 1 x 1 x 256 x 64 = 16384 2st layer : 3 x 3 x 64 x 64 = 36864 3st layer : 1 x 1 x 64 x 256 = 16384 total parametr : 70k |
파라미터 갯수는 Bottle Neck 이 더 적은데 채널 갯수는 4배 차이나는걸 확인할 수 있다.
만약 Not Bottle도 Bottle과 마찬가지로 256 개 채널을 입력하고 convolution으로 64개 채널을 계산한 이후에 다시 256개 output channel로 출력하는 형태라고 한다면 파라미터 갯수가 2배 넘게 차이나게 된다. ( 3 x 3 x 256 x 64 를 두 번 더하면 약 30k)
그 외 추가로 CIFAR-10 데이터셋을 가지고 학습 및 비교해본 내용,
Pascal, MS COCO 데이터셋을 가지고 학습 및 비교해본 내용 을 다루고 있습니다.
적은 이미지에 대해 1000 층이 넘는 ResNet으로 학습해본 결과 OverFitting으로 인해 오히려 성능이 저하되더라 하는 내용 또한 알아두어야겠네요.
* 풀잎스쿨 딥러닝 논문 요약 및 구현 스터디에서 진행한 내용 입니다.
* 나동빈씨 유투브를 참고하였습니다. 샤라웃 동빈나! (https://www.youtube.com/watch?v=671BsKl8d0E)
'DL' 카테고리의 다른 글
| [YOLO; You Only Look Once] Unified, Real-Time Object Detection (0) | 2023.06.29 |
|---|---|
| 순환 신경망 실습 (0) | 2023.06.25 |
| [Transformer] Attention is all you need (보완 예정) (0) | 2023.06.22 |
| Docker를 통한 Jupyter Notebook 접속 (0) | 2023.05.04 |
| 학습환경 세팅 ( Docker ) (0) | 2023.05.04 |
