[1로 만들기]
정수 X를 입력해, 5 로 나누거나, 3으로 나누거나, 2 로 나누거나, 1을 빼는 연산을 반복하여 1을 갖겠끔 하는 최단 연산의 갯수를 구하시오
- 도식화를 해보고 느낀 점은 1부터 해서 바텀 업 연산을 해야겠다.
- 1부터 X값 까지 최단 연산의 갯수를 다 구하면 되지 않을까?
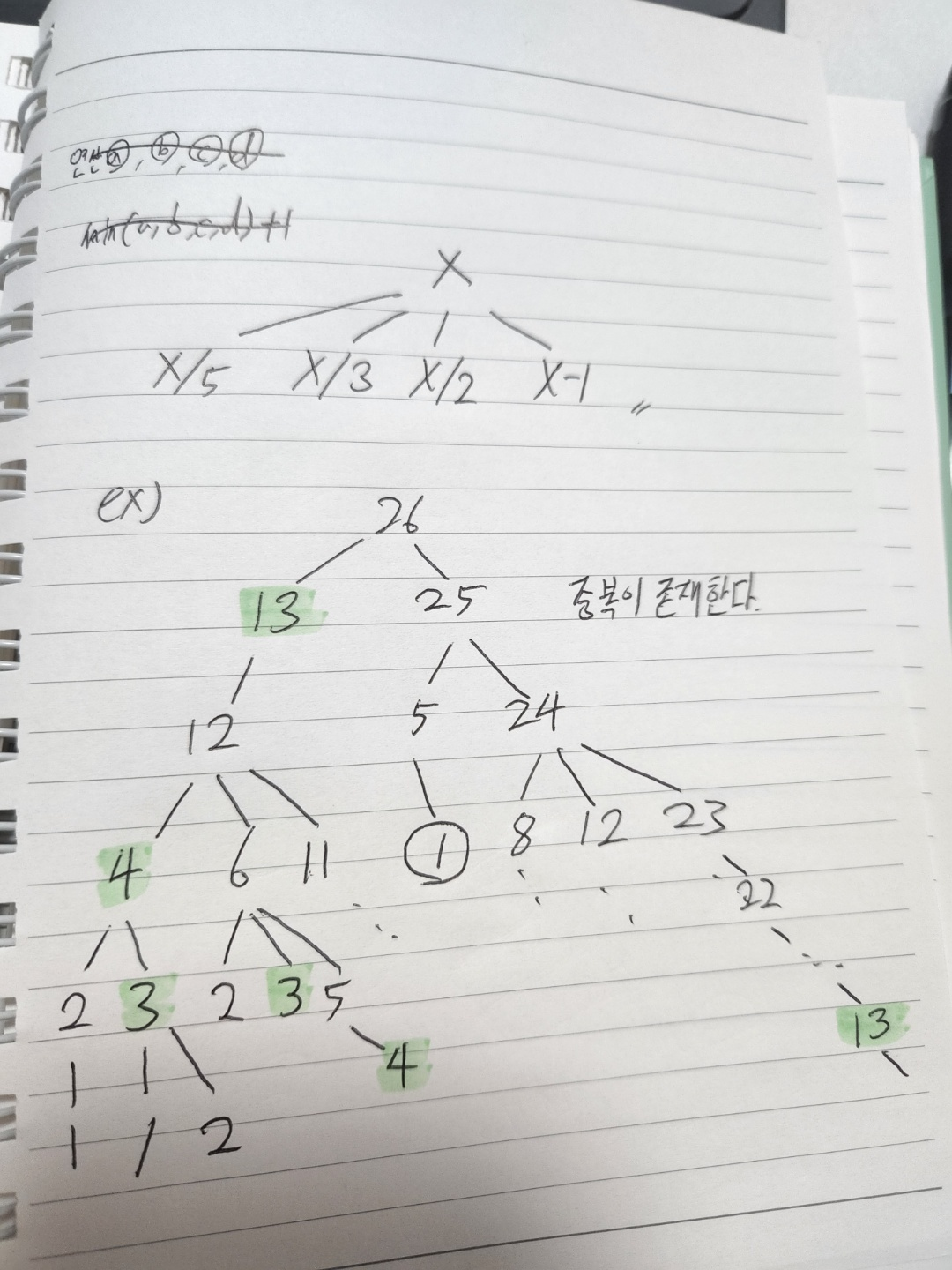
근데 어떻게 연산 갯수 세는걸 어떻게 구현해야할지 모르겠어서 책을 봤다.
( 졸면서 5시간 고민 했는데 점화식이라는 개념이 미쳐 떠오르지 않았다. )
- 점화식을 구해서 : \( a_i = min(a_{i-1},a_{i/2},a_{a/3},a_{a/5})+1 \)
- 점화식을 토대로 소스 코드를 작성한다.
def sol(X):
# df 테이블 초기화, d[1] = 0
d = [0]*(X+1)
for i in range(1,X+1):
d[i] = d[i] + 1
if i % 5 == 0:
d[i] = min( d[i], d[i/5]+1 )
if i % 3 == 0:
d[i] = min( d[i],d[i/3]+1 )
if i % 2 == 0:
d[i] = min( d[i],d[i/2]+1 )
print(d[X])
5로 나누는 연산, 3으로, 2로, .. 다 해봐야했는데 무척 깔끔하게 코드가 작성됐다.
min 함수를 어떻게 쓰는건지랑 바텀업 방식이 어떤건지 손에 새기고 가야겠다.
[개미 전사]
개미가 일직선 창고를 터는데 인접한 창고는 못 턴다. 가령 창고가 2 3 1 로 이루어져 있으면, 개미는 2와 1 또는 3 을 털 수 있다. 이때 개미가 터는 식량의 최댓값을 구하는 문제.
- n 번째 창고에 대하여, n 번째 창고를 털 경우 개미는 n-1번째 창고와 n+1번째 창고를 털지 못한다.
- n 번째 창고를 털지 말지에 대한 의사 결정과 n+1 번째 창고를 털지 말지에 대한 의사결정 과정의 논리 구조가 동일하다. 따라서 다이나믹 프로그래밍 문제이다.
- 점화식을 생각해보기 위해 무작위의 숫자를 나열하여 n번째와 n+1번째, n+2번째 와의 관계 등에 대해 고민해 보았다.

- 이를 코드로 구현해보자.
- 점화식에 쓰이는 수열은 dp 테이블 이라고 생각하고 저장해나가면 될 것 같다.
- 둘 중에 큰 값 비교하여 넣는건 max() 를 쓰면 된다.
- 이제 조금씩 DP 문제가 감이 잡히는 기분이다.
def sol(array):
d = [0]*1000
d[0] = array[0]
d[1] = max(array[0],array[1])
for i in range(2,len(array)):
d[i] = max(d[i-1],d[i-2]+array[i])
print(d[len(array)-1])
array = [1,3,1,5]
sol(array)
[바닥 공사]
가로 길이가 N이고 세로 길이가 2인 직사각형 형태의 얇은 바닥에 대해 1*2 의 덮개, 2*1의 덮개, 2*2의 덮개로 채우고자 한다.
- 문제에 대해 n과 n-1, .. 의 관계로 나눌 수 있고, 이에 대한 점화식을 세울 수 있는거면 다이나믹 프로그래밍으로 해결 가능하다.
- 학생 때 배운 귀납법적인 증명과정이 곧 다이나믹 프로그래밍으로 풀 수 있는 과정을 말하는 거였다.
- 처음에는 점화식을 다음과 같이 세웠다.
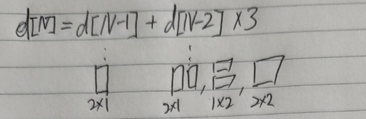
( d[N-1]에 2*1 타일이 붙으면 가로 N 타일 완성, d[N-2] 아래 그림 또한 마찬가지 의미 )
그러나 테스트 케이스로 3을 넣어보자, output이 5여야 하는데 6이 나왔다.
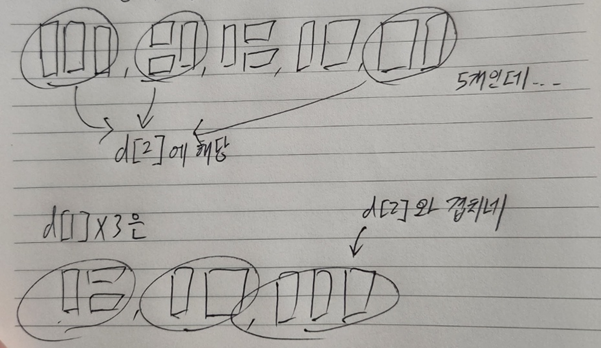
그림을 그려보니
다음과 같은 케이스가 서로 중복되어 나타남을 알았다.
d[N-1] 에다가 1*2 타일을 더할 때와
d[N-2] 에다가 1*2 타일 두 번 더할 때의 케이스 중에 겹치는 케이스가 나오는 것이다.
앞의 케이스가 뒤의 케이스를 포괄하므로
점화식을 다음과 같이 수정해준다.
\( d[N] = d[N-1] + d[N-2]*2 \)
이를 코드로 구현해주면 끝.
def sol(N):
d = [0]*(1001)
d[1] = 1
d[2] = 3
for n in range(3,N+1):
d[n] = d[n-1]+d[n-2]*2
print(d[N]%796796)
sol(3)[효율적인 화폐 구성]
화폐 종류와 만들어야 하는 금액을 N, M으로 주어준다.
그리고 화폐 종류가 주어진다.
가령 )
2 15
2
3
이면 2가지 화폐 종류 (2, 3) 으로 15를 만들어야하는데, 최소의 갯수를 쓴다고 하면 3을 5번 쓰면 되므로 답은 5 이다.
화폐를 못만들 경우 -1을 출력한다.
- 그리디 알고리즘 같지만, 화폐의 큰 단위가 작은 단위의 배수가 아니기 때문에 그리디 문제는 아니다.
- 그리디는 큰 단위를 택했다고 해서 최적의 해가 안나오고 그런 상황이 발생하면 안된다.
- 처음에는 무턱대놓고 숫자를 나열한 뒤 관계를 찾으려고 했다.
- 그러나 그렇게 풀면 안되고, 앞서 말했던 귀납법 문제 풀듯이 해야 답을 구할 수 있다.
- m은 만들어야하는 금액, 2 와 3을 주어진 화폐 종류라고 하자
- \( a_m = min(a_{m-2} + 1 , a_{m-3}+1) \)
- 점화식이 다음과 같이 완성 되었다. 이제 코드로 구현해보자.
- 만약 m을 만들지 못하는 경우에는 어떻게 해야되냐? 최대 M값보다 1 큰 10001 정도로 설정하면 되겠다.
def sol(N,M,coin_list):
d = [10001]*10001
d[0] = 0
for i in range(N):
d[coin_list[i]] = 1
for i in range(M+1):
for j in range(N):
d[i] = min(d[i], d[i-coin_list[j]]+1) # 인덱스 마이너스 값 나와도 어차피 충분히 리스트가 길어서 10001 나오기 때문에 문제 없다.
if d[i] == 10001:
print(-1)
else: print(d[M])
N, M = 3, 4
coin_list = [3,5,7]
sol(N,M,coin_list)
참고한 책 ; 나동빈 (2020). <이것이 취업을 위한 코딩 테스트다 with 파이썬>. 서울시: 한빛미디어.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 최단 경로 플로이드 워셜 알고리즘 (0) | 2022.06.21 |
|---|---|
| [알고리즘] 다익스트라 최단경로 알고리즘 (0) | 2022.06.19 |
| [알고리즘] 다이나믹 프로그래밍 (0) | 2022.06.11 |
| [알고리즘] DFS, BFS (0) | 2022.06.07 |
| [알고리즘] 구현 실습, 개임 게발 (이코테) (0) | 2022.05.30 |
