[그래프]
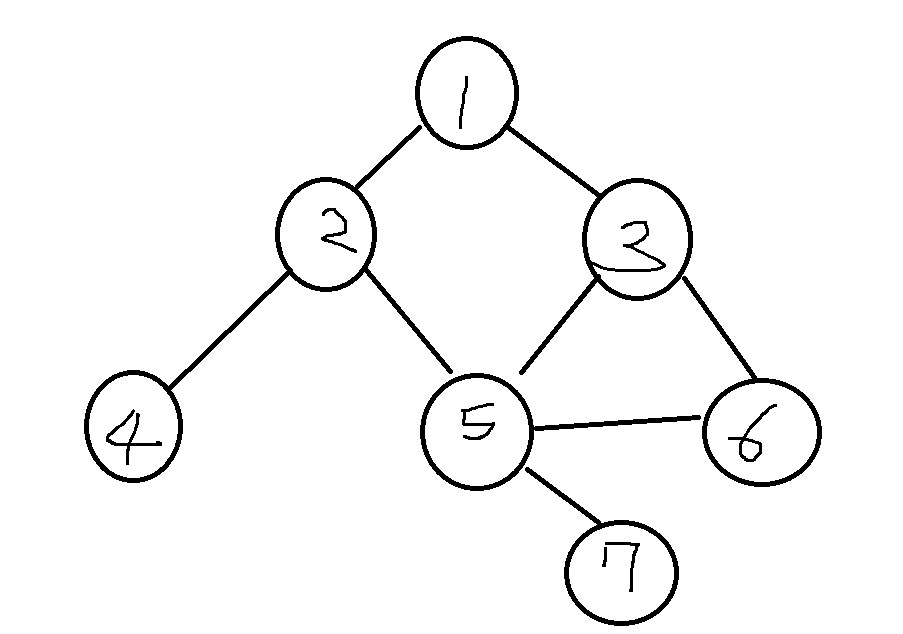
- 그래프는 크게 두가지 형태로 그릴 수 있습니다. 위의 예시를 가지고 다뤄보도록 할게요
참고로, 인덱스 0에 해당하는 값들을 헷깔리지 않게 일부로 비운 상태로 더 만들었습니다.
- 인접행렬
양방향일 때 인접행렬은 늘 대칭입니다. 이를 이용하면 조금 더 쉽게 정리할 수 있을 것 같습니다.
graph = [
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 0, 0, 0, 0], # 1행
[0, 1, 0, 0, 1, 1, 0, 0], # 2행
[0, 1, 0, 0, 0, 1, 1, 0], # 3행
[0, 0, 1, 0, 0, 0, 0, 0], # 4행
[0, 0, 1, 1, 0, 0, 1, 1], # 5행
[0, 0, 0, 1, 0, 1, 0, 0], # 6행
[0, 0, 0, 0, 0, 1, 0, 0], # 7행
]
- 인접리스트
인덱스 0인 부분을 일부로 비워 헷깔리지 않게 만들었습니다.
graph = [
[],
[2,3], # 1행
[1,4,5], # 2행
[1,5,6], # 3행
[2], # 4행
[2,3,6,7], # 5행
[3,5], # 6행
[5], # 7행
][DFS]
1. 깊이 순으로 탐색하는 알고리즘 입니다.
2. 루트 노드에서 시작하여 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색합니다.
3. 검색 속도 자체는 BFS 보다 느리다고 합니다.

- 스택을 활용하면 조금 더 쉽게 이해할 수 있습니다.
- 1부터 탐색을 시작하고, 작은 숫자를 보다 우선하는 DFS 탐색을 본다고 할 때,
# 스택에는 다음과 같이 들어갑니다.
[ ]
[ 1 ] # 노드 1를 넣고
[ 1, 2 ] # 노드 1 과 이어진 2를 넣고
[ 1, 2, 4 ] # 노드 2 과 이어진 4를 넣고
[ 1, 2 ] # 노드 4 에서는 갈 곳이 없으므로 노드 4를 스택에서 뺍니다.
[ 1, 2, 5 ] # 노드 2 과 이어진 5를 넣고
[ 1, 2, 5, 3 ] # 노드 5 와 이어진 3을 넣고
[ 1, 2, 5, 3, 6 ] # 노드 3 과 이어진 6을 넣고
[ 1, 2, 5, 3 ] # 노드 6 에서 갈 곳이 없으므로 노드 6을 스택에서 뺍니다.
[ 1, 2, 5 ] # 노드 3 에서 갈 곳이 없으므로 노드 3을 스택에서 뺍니다.
[ 1, 2, 5, 7 ] # 노드 5 와 이어진 7을 넣고
[ 1, 2, 5 ] # 탐색이 끝났으므로 더 이상 갈 곳은 없고 이제 순차적으로 스택에서 뺍니다.
[ 1, 2 ]
[ 1 ]
[ ]
# 1 -> 2 -> 4 -> 5 -> 3 -> 6 -> 7
재귀함수 통한 DFS 구현
def DFS(graph, visited, v):
visited[v] = True
print(v, end= ' ')
for i in range(len(graph[v])):
if not visited[graph[v][i]] :
DFS(graph, visited, graph[v][i])
visited = [False for _ in range(8)]
DFS(graph, visited, 1)
한 가지 신기했던 건 visited에 global 선언을 안해줬다는 것
관련 내용 정리 ) https://callmescone.tistory.com/142
[파이썬] mutable은 global 변수인가?
imutable한 객체(bool, int, float, str, tuple) 의 경우 연산자를 사용해 값을 변경하려 할 때 마다 새로운 객체를 생성에서 할당한다. mutable 한 객체 (dict, list, set)는 재할당하지 않고 값을 변경한다고 한..
callmescone.tistory.com
[BFS]
1. 인접한 노드를 우선 탐색합니다.
2. 주로 두 노드 사이의 최단 경로를 찾고자 할 때 이 방법을 선택합니다.
ex) 지구 상에 있는 모든 친구 관계가 선으로 이어져 있을 때, 스콘과 로버트 다우니 주니어 사이에 존재하는 최단경로를 찾는 경우 ( DFS의 경우 모든 친구 관계를 다 봐야할 수 있으나, BFS의 경우 스콘과 가까운 인간관계 부터 탐색합니다. )

- 큐를 활용하면 보다 쉽게 접근할 수 있습니다.
# 큐
[ ]
[ 1 ] # 노드 1부터 시작한다.
[ 2, 3 ] # 큐의 왼쪽에 있는 노드 1을 지우고, 1과 연결된 노드 2, 3을 추가한다.
[ 3, 4, 5 ] # 큐의 왼쪽에 있는 노드 2을 지우고, 2와 연결된 노드 4, 5를 추가한다.
[ 4, 5, 6 ] # 큐의 왼쪽에 있는 노드 3을 지우고, 3과 연결된 노드 6을 추가한다.
[ 5, 6 ] # 큐의 왼쪽에 있는 노드 4를 지우고, 4와 연결된 노드 가운데 방문하지 않은 노드가 없어서 추가하지 않는다.
[ 6, 7 ] # 큐의 왼쪽에 있는 노드 5를 지우고, 5와 연결된 노드 7을 추가한다.
[ 7 ] # 큐의 왼쪽에 있는 노드 6을 지운다.
[ ] # 큐의 왼쪽에 있는 노드 7을 지운다.
# 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7
from collections import deque
def BFS(startnode):
que = deque()
que.append(startnode)
visited[startnode] = True
while que:
v = que.popleft()
print(v,end=' ')
for i in graph[v]:
if not visited[i]:
que.append(i)
visited[i] = True
visited = [False for _ in range(8)]
BFS(1)[DFS V.S. BFS]
- 모든 노드를 검색한다는 점에서 두 알고리즘간 시간 복잡도는 동일하다.
| 인접 리스트 | \( O(N+E) \) |
| 인접 행렬 | \( O(N^2) \) |
- 문제 유형에 따른 분류
- 모든 정점 방문 : 둘 중 어느 것도 ok
- 경로의 특징 저장 : DFS를 사용한다.
- 최단거리 : BFS가 유리하다.
- 검색 대상 그래프가 정말 크다면 : DFS를 고려
- 검색 대상 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS를 고려
문제 유형에 따른 분류는 앞으로 문제를 접하면서 정리를 해나가야 의미가 있을 것 같다.
참고한 책 ; 나동빈 (2020). <이것이 취업을 위한 코딩 테스트다 with 파이썬>. 서울시: 한빛미디어.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 다이나믹 프로그래밍(DP) 교재 문풀 (0) | 2022.06.12 |
|---|---|
| [알고리즘] 다이나믹 프로그래밍 (0) | 2022.06.11 |
| [알고리즘] 구현 실습, 개임 게발 (이코테) (0) | 2022.05.30 |
| [알고리즘] 구현 (0) | 2022.05.30 |
| [알고리즘] 그리디 실습 (숫자 카드 게임, 1이 될 때 까지) (0) | 2022.05.22 |

[그래프]
- 그래프는 크게 두가지 형태로 그릴 수 있습니다. 위의 예시를 가지고 다뤄보도록 할게요
참고로, 인덱스 0에 해당하는 값들을 헷깔리지 않게 일부로 비운 상태로 더 만들었습니다.
- 인접행렬
양방향일 때 인접행렬은 늘 대칭입니다. 이를 이용하면 조금 더 쉽게 정리할 수 있을 것 같습니다.
graph = [
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 0, 0, 0, 0], # 1행
[0, 1, 0, 0, 1, 1, 0, 0], # 2행
[0, 1, 0, 0, 0, 1, 1, 0], # 3행
[0, 0, 1, 0, 0, 0, 0, 0], # 4행
[0, 0, 1, 1, 0, 0, 1, 1], # 5행
[0, 0, 0, 1, 0, 1, 0, 0], # 6행
[0, 0, 0, 0, 0, 1, 0, 0], # 7행
]
- 인접리스트
인덱스 0인 부분을 일부로 비워 헷깔리지 않게 만들었습니다.
graph = [
[],
[2,3], # 1행
[1,4,5], # 2행
[1,5,6], # 3행
[2], # 4행
[2,3,6,7], # 5행
[3,5], # 6행
[5], # 7행
][DFS]
1. 깊이 순으로 탐색하는 알고리즘 입니다.
2. 루트 노드에서 시작하여 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색합니다.
3. 검색 속도 자체는 BFS 보다 느리다고 합니다.

- 스택을 활용하면 조금 더 쉽게 이해할 수 있습니다.
- 1부터 탐색을 시작하고, 작은 숫자를 보다 우선하는 DFS 탐색을 본다고 할 때,
# 스택에는 다음과 같이 들어갑니다.
[ ]
[ 1 ] # 노드 1를 넣고
[ 1, 2 ] # 노드 1 과 이어진 2를 넣고
[ 1, 2, 4 ] # 노드 2 과 이어진 4를 넣고
[ 1, 2 ] # 노드 4 에서는 갈 곳이 없으므로 노드 4를 스택에서 뺍니다.
[ 1, 2, 5 ] # 노드 2 과 이어진 5를 넣고
[ 1, 2, 5, 3 ] # 노드 5 와 이어진 3을 넣고
[ 1, 2, 5, 3, 6 ] # 노드 3 과 이어진 6을 넣고
[ 1, 2, 5, 3 ] # 노드 6 에서 갈 곳이 없으므로 노드 6을 스택에서 뺍니다.
[ 1, 2, 5 ] # 노드 3 에서 갈 곳이 없으므로 노드 3을 스택에서 뺍니다.
[ 1, 2, 5, 7 ] # 노드 5 와 이어진 7을 넣고
[ 1, 2, 5 ] # 탐색이 끝났으므로 더 이상 갈 곳은 없고 이제 순차적으로 스택에서 뺍니다.
[ 1, 2 ]
[ 1 ]
[ ]
# 1 -> 2 -> 4 -> 5 -> 3 -> 6 -> 7
재귀함수 통한 DFS 구현
def DFS(graph, visited, v):
visited[v] = True
print(v, end= ' ')
for i in range(len(graph[v])):
if not visited[graph[v][i]] :
DFS(graph, visited, graph[v][i])
visited = [False for _ in range(8)]
DFS(graph, visited, 1)
한 가지 신기했던 건 visited에 global 선언을 안해줬다는 것
관련 내용 정리 ) https://callmescone.tistory.com/142
[파이썬] mutable은 global 변수인가?
imutable한 객체(bool, int, float, str, tuple) 의 경우 연산자를 사용해 값을 변경하려 할 때 마다 새로운 객체를 생성에서 할당한다. mutable 한 객체 (dict, list, set)는 재할당하지 않고 값을 변경한다고 한..
callmescone.tistory.com
[BFS]
1. 인접한 노드를 우선 탐색합니다.
2. 주로 두 노드 사이의 최단 경로를 찾고자 할 때 이 방법을 선택합니다.
ex) 지구 상에 있는 모든 친구 관계가 선으로 이어져 있을 때, 스콘과 로버트 다우니 주니어 사이에 존재하는 최단경로를 찾는 경우 ( DFS의 경우 모든 친구 관계를 다 봐야할 수 있으나, BFS의 경우 스콘과 가까운 인간관계 부터 탐색합니다. )

- 큐를 활용하면 보다 쉽게 접근할 수 있습니다.
# 큐
[ ]
[ 1 ] # 노드 1부터 시작한다.
[ 2, 3 ] # 큐의 왼쪽에 있는 노드 1을 지우고, 1과 연결된 노드 2, 3을 추가한다.
[ 3, 4, 5 ] # 큐의 왼쪽에 있는 노드 2을 지우고, 2와 연결된 노드 4, 5를 추가한다.
[ 4, 5, 6 ] # 큐의 왼쪽에 있는 노드 3을 지우고, 3과 연결된 노드 6을 추가한다.
[ 5, 6 ] # 큐의 왼쪽에 있는 노드 4를 지우고, 4와 연결된 노드 가운데 방문하지 않은 노드가 없어서 추가하지 않는다.
[ 6, 7 ] # 큐의 왼쪽에 있는 노드 5를 지우고, 5와 연결된 노드 7을 추가한다.
[ 7 ] # 큐의 왼쪽에 있는 노드 6을 지운다.
[ ] # 큐의 왼쪽에 있는 노드 7을 지운다.
# 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7
from collections import deque
def BFS(startnode):
que = deque()
que.append(startnode)
visited[startnode] = True
while que:
v = que.popleft()
print(v,end=' ')
for i in graph[v]:
if not visited[i]:
que.append(i)
visited[i] = True
visited = [False for _ in range(8)]
BFS(1)[DFS V.S. BFS]
- 모든 노드를 검색한다는 점에서 두 알고리즘간 시간 복잡도는 동일하다.
| 인접 리스트 | \( O(N+E) \) |
| 인접 행렬 | \( O(N^2) \) |
- 문제 유형에 따른 분류
- 모든 정점 방문 : 둘 중 어느 것도 ok
- 경로의 특징 저장 : DFS를 사용한다.
- 최단거리 : BFS가 유리하다.
- 검색 대상 그래프가 정말 크다면 : DFS를 고려
- 검색 대상 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS를 고려
문제 유형에 따른 분류는 앞으로 문제를 접하면서 정리를 해나가야 의미가 있을 것 같다.
참고한 책 ; 나동빈 (2020). <이것이 취업을 위한 코딩 테스트다 with 파이썬>. 서울시: 한빛미디어.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 다이나믹 프로그래밍(DP) 교재 문풀 (0) | 2022.06.12 |
|---|---|
| [알고리즘] 다이나믹 프로그래밍 (0) | 2022.06.11 |
| [알고리즘] 구현 실습, 개임 게발 (이코테) (0) | 2022.05.30 |
| [알고리즘] 구현 (0) | 2022.05.30 |
| [알고리즘] 그리디 실습 (숫자 카드 게임, 1이 될 때 까지) (0) | 2022.05.22 |
