[백준 9단계] 11729 하노이의 탑 이동 순서

🥕 [ 백준 11729 ] 하노이의 탑 이동 순서

문제 링크

url : https://www.acmicpc.net/problem/11729

11729번: 하노이 탑 이동 순서

 

🍒 문제 분석

유명한 하노이의 탑 이동 문제 입니다.

작은 원판 위에는 큰 원판을 올릴 수 없고, 한번에 하나의 원판만을 옮길 수 있으며,

최적의 동선으로 1에서 3으로 탑을 옮겨야만 하죠.

🥑 코드

def moveDisc(cnt, from_bar, to_bar, via_bar):
    global anslist
    if cnt == 1:
        anslist.append([from_bar,to_bar])
    else:
        moveDisc(cnt-1,from_bar,via_bar,to_bar)
        moveDisc(1,from_bar,to_bar,via_bar)
        moveDisc(cnt-1,via_bar,to_bar,from_bar)

cnt = int(input())
anslist = []
moveDisc(cnt,1,3,2)
print(len(anslist))
for li in anslist:
    print(f'{li[0]} {li[1]}')

 

🍓 내 해결 과정

그림을 그렸다.

 

moveDisc(cnt-1,from_bar,via_bar,to_bar)

moveDisc(1,from_bar,to_bar,via_bar)

moveDisc(cnt-1,via_bar,to_bar,from_bar)

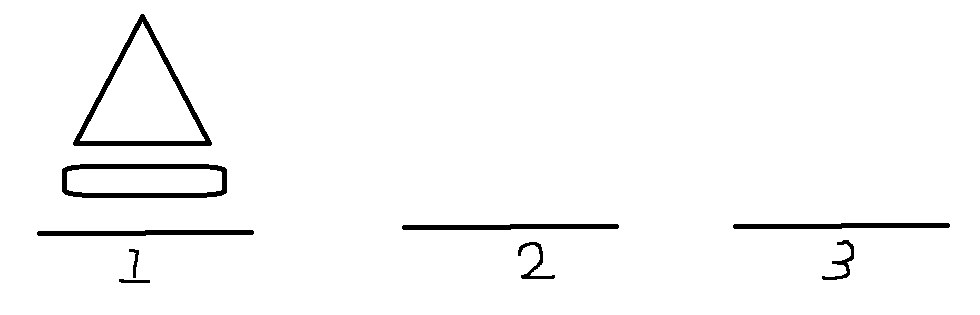
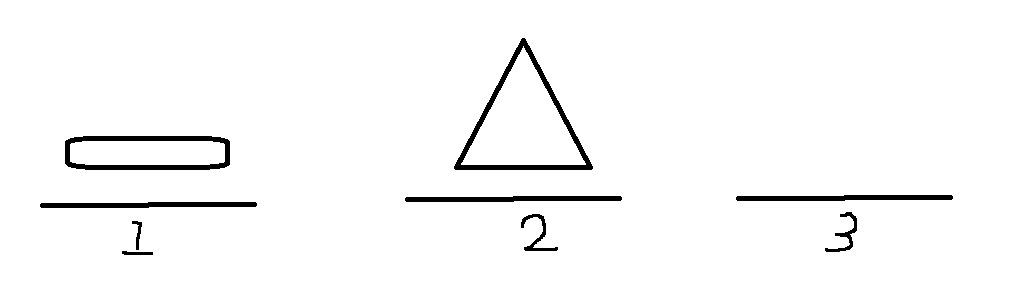
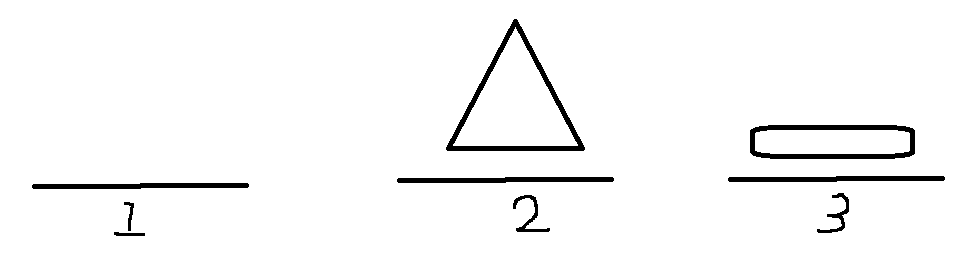
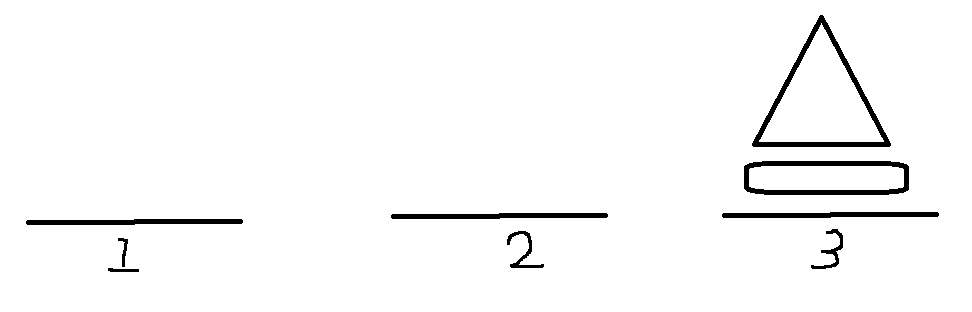
1. 1번(from)에서 원판 하나 빼고 나머지 것들을 2번(경유지)으로 옮긴다. ; 함수 호출

2. 1번(from)에 남은 원판을 3번(to) 로 옮긴다. ; 함수 호출

3. 2번(via)에 있는 원판들을 3번(to)으로 옮긴다. ; 함수 호출

 

이처럼 하나의 함수 안에 재귀 호출 3번이 이루어진다.

다만 원판이 1개 일때는 더 이상 재귀 호출을 하지 않으므로 값을 반환해주거나 또는 실행하고자 하는 바를 써야 한다는 것에 유의 한다.

 

🌽 다른 사람 코드

cache = {}

def h(f, v, t, n):
    if n == 1:
        return f'{f} {t}\n'      # f-string
    if (f, v, t, n) in cache:
        return cache[(f, v, t, n)]
    else:
        cur = [h(f, t, v, n - 1), f'{f} {t}\n', h(v, f, t, n - 1)]
        cache[(f, v, t, n)] = ''.join(cur)
        return cache[(f, v, t, n)]


N = int(input())
sum = 1
for i in range(N-1):
    sum = sum*2 + 1
print(sum)
print(h(1, 2, 3, N))

1. 처음에는 재귀를 통해 경로를 딕셔너리에 저장한다.

2. 만약 동일한 경로를 불러올 경우, 딕셔너리에 저장되어 있는 경로일 경우 고대로 불러온다.

3. 재귀를 몇번 호출하느냐는 주어진 cnt에 대한 규칙성을 이용해 계산하여 프린트했다.

 

🍉 깨달은 점 및 정리

1. 하노이 탑 이동 재귀함수를 쓰는 법을 알았다.

2. 딕셔너리 활용은 연습을 좀 더 해서 능숙해졌을 때야 가능하겠다.