[백준 그래프이론] 1600 말이 되고픈 원숭이

🥕 [ 백준 1600 ] 말이 되고픈 원숭이

문제 링크

url : https://www.acmicpc.net/problem/1600

1600번: 말이 되고픈 원숭이

 

🍒 문제 분석

원숭이는 체스의 나이트와 같은 이동 방식을 가진다.

단, K번만 그럴 수 있고, 그 외에는 인접한 네칸 으로만 움직일 수 있다.( 위, 아래, 왼쪽, 오른쪽 )

원숭이가 최소한의 동작으로 시작지점에서 도착지점 까지 갈 수 있는 방법을 알아내는 프로그램을 작성해보는 문제이다.

 

최소한의 동작으로 목적지를 도착 한다는건 다시말해

BFS 알고리즘으로 풀면 된다는 의미로 받아들이면 될 것 같다.

 

BFS 알고리즘 을 생각한 이유

1. 왜냐면 간선의 cost를 계산해야 하는 것도 아니라는 점.

2. 현재 위치하고 있는 노드를 기준으로 갈 수 있는 곳들을 다 q에 넣고 넣은 q들 다 빼고 다시 넣을 때,

3. 동작 값을 1씩 추가하는 방식으로 계산하면 도착지점 까지 가장 먼저 도착하는 경로를 찾을 수 있다.

 

이제 고려해야할 점으로

1. 단순히 인접한 4방향 뿐만 아니라 체스의 나이트 처럼도 이동할 수 있다는 점

2. 체스의 나이트 처럼 이동하는데 K번의 제약 조건이 있다는 점

3. 인접한 4방향으로 이동할 때와 체스의 나이트 처럼 이동할 때 간에 동선이 서로 겹칠 수 있다는 점.

 

따라서 접근 방식

1. BFS 알고리즘을 쓰자.

2. direction 리스트를 인접한 4방향 버전과 체스의 나이트 버전으로 만들어야겠다.

3. 방문한 곳, visited를 표시할 때 인접한 4방향으로 이동해서 간 버전과 체스의 나이트 버전으로 해서 만들어야겠다.

 

이제 문제를 풀어보겠습니다.

 

🥑 코드

from collections import deque

# 인접한 4곳
md = [(-1,0),(1,0),(0,1),(0,-1)]

# 말의 이동 방향
hd = [(2,1),(1,2),(-1,2),(-2,1),(-2,-1),(-1,-2),(1,-2),(2,-1)]

def check_visit(nx, ny, nk):
    if 0<=nx<H and 0<=ny<W and not visited[nx][ny][nk] and graph[nx][ny] == 0 :
        return True   # 가도 됨
    return False      # 가면 안됨

def bfs():
    q = deque()
    q.append([0,0,0])
    while q:
        x, y, k = q.popleft()

        # 도착점인 경우
        if x==(H-1) and y==(W-1):
            # 처음에 시작점에서 동작수에 1를 매겨줬기 때문에 1을 빼준다.
            return visited[x][y][k] - 1
        
        # 인접한 곳으로 움직일 때
        for i in range(4):
            nx = x + md[i][1]
            ny = y + md[i][0]

            if check_visit(nx,ny,k):     # 가도 되면
                q.append([nx,ny,k])      # 간다.
                visited[nx][ny][k] = visited[x][y][k] + 1
        
        # 말처럼 움직일 때
        if k < K:
            for i in range(8):
                nx = x + hd[i][1]
                ny = y + hd[i][0]
                nk = k + 1
                if check_visit(nx,ny,nk):
                    q.append([nx,ny,nk])
                    visited[nx][ny][nk] = visited[x][y][k] + 1
    return -1



# 말 처럼 이동 가능한 횟수
K = int(input())

# W 열 갯수(가로길이) => y, H 행 갯수(세로 길이) =>x
W, H = map(int, input().split())

# graph[행][열] => graph[H][W] => graph[x][y] 
graph = [list(map(int,input().split())) for _ in range(H)]

# 말의 이동을 고려하기 위한 3차원 배열
visited = [[[0]*(K+1) for _ in range(W)] for _ in range(H)]

# 시작점 방문
visited[0][0][0] = 1

print(bfs())

🍓 내 해결 과정

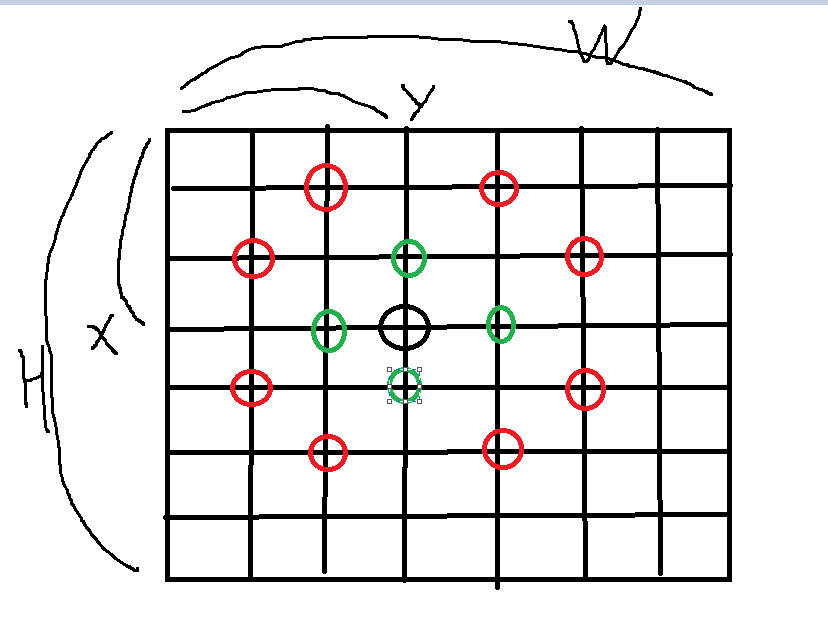
초록색 : 인접한 4곳

빨간색 : 말처럼 갈 수 있는 곳 8곳

 

저렇게 12개의 위치가 현재 위치(검은색) 에서 갈 수 있는 다음 노드가 됩니다.

 

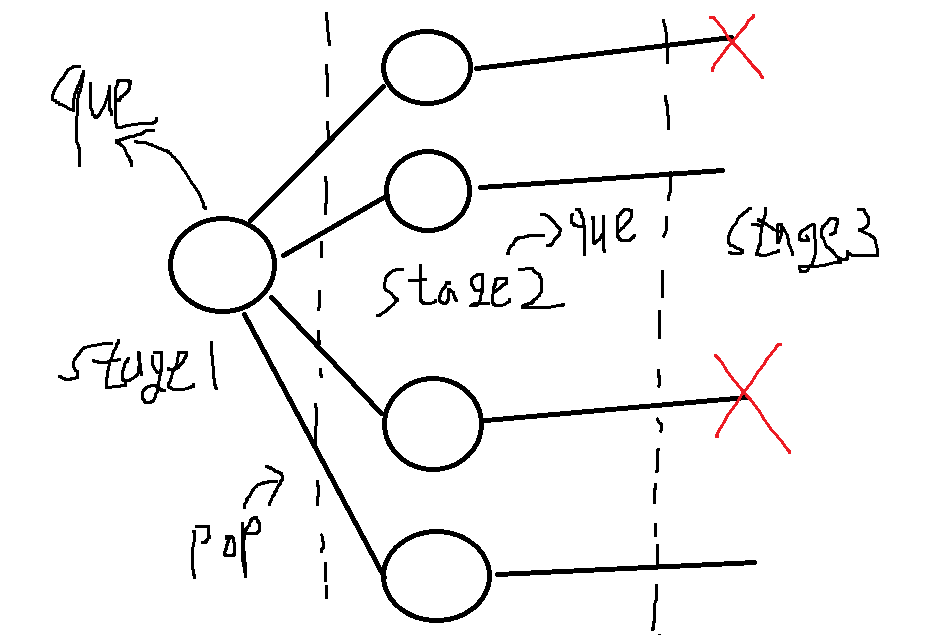
bfs  알고리즘이기 때문에 순서는 다음과 같습니다.

1. stage1 의 노드를 que에 넣고

2. que를 pop 한 뒤, 거기서 갈 수 있는 모든 노드를 que에 넣습니다.

3. 그럼 stage2의 노드들이 que에 들어가게 되고

4. 다시 stage2의 노드들을 pop하면 stage 3의 노드들이 que에 들어가게 됩니다.

 

stage는 원숭이가 움직인 횟수를 의미합니다.

따라서 stage1 -> stage2 -> .. 를 거치다가 목적지에 도착하면 움직인 횟수를 반환하고

 

원숭이가 더 이상 갈 곳이 없게 되면 다음 stage가 존재하지 않기 때문에 que가 텅 비게 되고

알고리즘이 끝나며 따라서 -1을 반환합니다.

 

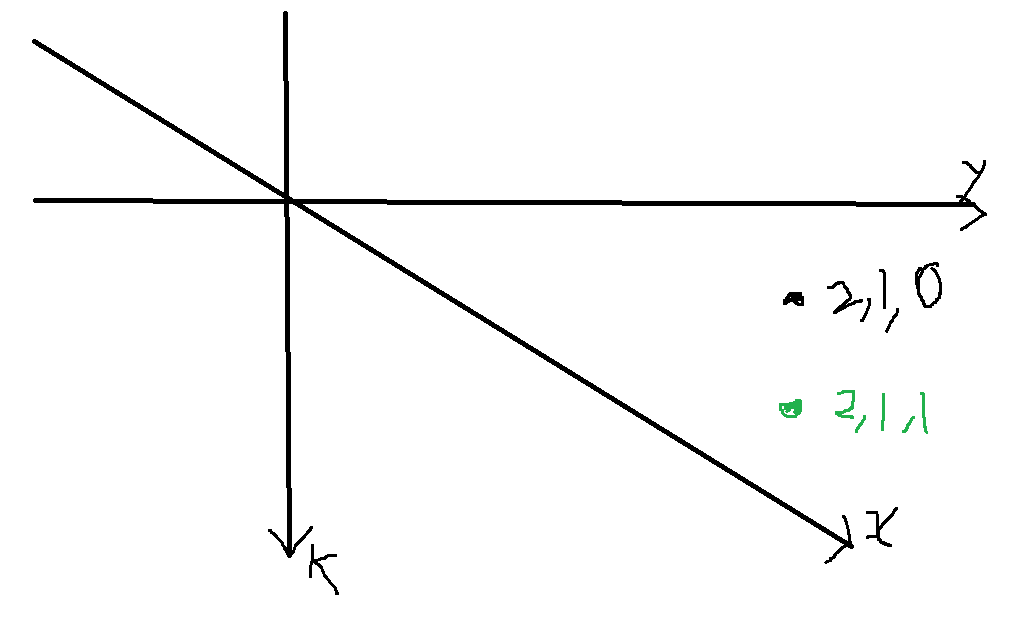
visited 테이블의 형태는 다음과 같습니다.

3차원 배열입니다.

 

검은색 점은 (2, 1, 0) 으로 말의 움직임 없이 원숭이가 좌표 2,1 에 도착한걸 의미하죠.

원숭이의 움직임으로는 좌표 2,1 까지 3번에 걸쳐 가야하므로 visited[2][1][0] 에는 값이 4가 적히게 될 겁니다.

 

초록색 점은 (2,1,1) 으로 말의 움직임을 한번 써서 좌표 2,1 에 도착한 걸 의미합니다.

start 위치 좌표 0, 0 에서 말의 움직임으로 한번에 좌표 2,1에 도착할 수 있으니 visited[2][1][1] 에는 값이 2가 적히게 되는거죠.

 

왜냐면 좌표 0,0 에 값이 1이 적혀있었는데 그 상태에서 한칸 이동한 것이니 1만큼 더해져 2가 되는 것입니다.

 

다음처럼 visited table을 3차원 배열로 만들게 되면 원숭이가 말의 움직임을 한 번 써서 그 좌표에 도착한 것인지 아니면 그냥 도착한 것인지,  그것도 아니면 말의 움직임을 2번 써서 도착한 것인지 등을 알 수 있게 됩니다.

 

만약 visited 값이 True 라면 이미 방문한 셈이니 그 곳에는 갈 수 없지만, 말의 움직임을 쓰지 않고는 그 곳에 간 적은 없기 때문에 이를 모두 고려해주기 위해 3차원 배열로 만들게 된 것입니다.

 

 

🍉 깨달은 점 및 정리

1. 최소 동작으로 어느 목적지에 도착하는 문제에 bfs 알고리즘을 쓸 수 있다.

2. 목적지 까지 가는 수단이 두개 이상이고 이를 혼용 할 수 있다면, visited table을 n차원으로 구성해보자.