🥕 [ 백준 2850 ] 나무 자르기
문제 링크
url : https://www.acmicpc.net/problem/2805
2805번: 나무 자르기
첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000) 둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M보
www.acmicpc.net
🍒 문제 분석
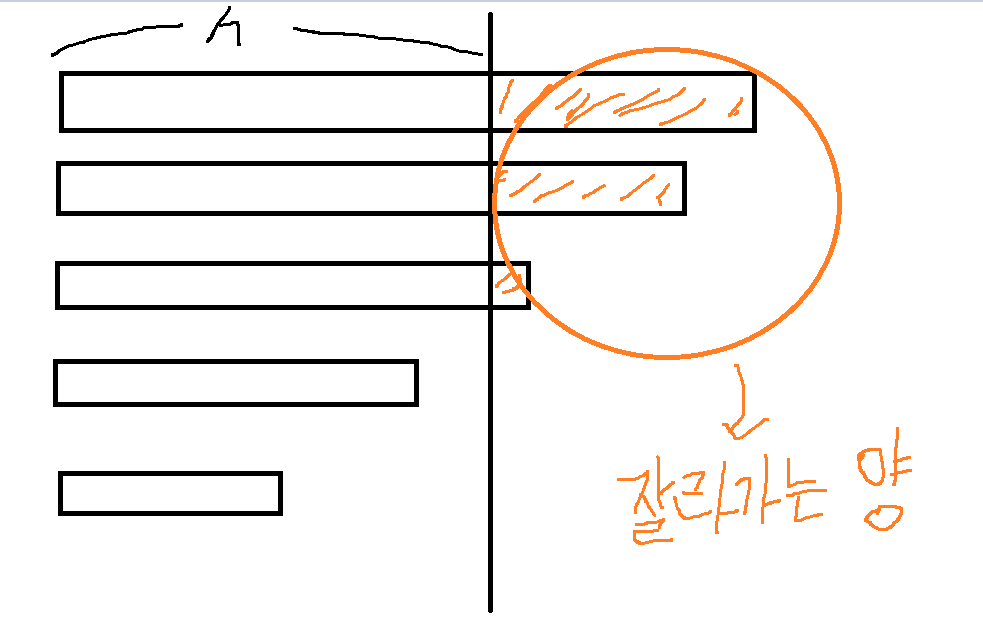
필요한 양이 M 이라고 할 때
h 만큼의 높이를 잘라 잘리는 부분 ( 주황색 ) 의 합이 M보다 크면 되는 문제이다.
나무의 갯수는 100만개 까지, 나무의 높이는 20억 까지 있다. 그리고 제한 시간은 1초이다.
주어진 input은 크면서 시간이 적기 때문에 문제 풀이로서 떠올릴 수 있는 방법은 한정 되어있다.
1. 파라메트릭 서치
- 최적화 문제를 결정 문제로 바꾸어 해결하는 기법
( 결정 문제란 예, 아니오 로 답하는 문제를 말한다. ) - 원하는 조건을 만족하는 가장 알맞은 값을 찾는 문제
2. DP
- 최적화 문제를 푸는 방법
이코테 책에 따르면(202p),
높이가 10억일 때, 만약 이진 탐색으로 높이 H를 구하고자 한다면 대략 31번에 모든 경우의 수를 고려할 수 있다고 한다.
그리고 나무의 갯수가 최대 100만개라면, 이진 탐색으로 높이 H를 바꾸면서, 바꿀 때마다 모든 나무를 체크한다고 하면 최대 3,000만 번 정도의 연산으로 문제를 풀 수 있다고 한다. 3,000만 번의 연산이면 최악의 경우, 아슬아슬하게 약 2초가 걸린다고 한다.
본 문제에서는 주어진 조건이 1초여서, 좀 곤란해 보이는데... 잘 모르겠다 일단 풀어보자.
나는 먼저 DP로 문제를 해결하였고, 후에 파라메트릭 서치를 찾아보게 되었다.
본 리뷰는 파라 메트릭 서치를 먼저 한 후, DP에 대한 풀이 방법을 적고자한다.
( DP래 봤자 그냥 군수열 점화식 쓴거라서 별거 없다. )
🥑 파라메트릭 서치
import sys
input = sys.stdin.readline
write = sys.stdout.write
# 나무 수, 가져가려는 나무 길이
N, M = map(int, input().split())
# 나무 높이들
array = list(map(int,input().split()))
array.sort()
# 이진탐색
start = 1
end = max(array)
result = 0
while(start <= end):
total = 0
mid = (start + end)//2
for tree in array:
if tree > mid:
total += tree - mid
if total > M:
start = mid + 1
elif total < M :
end = mid - 1
else:
end = mid
break
print(str(end))
1. 높이 H를 임의로 중간 값(mid)으로 정하여 놓고 계산
2. 가져가는 양이 충분치 않으면 높이 H를 줄여야함.
높이 H 를 다시 start와 mid-1 의 중간값으로 놓고 다시 탐색
3. 가져가는 양이 너무 많다면 높이 H를 늘려야함
높이 H를 다시 mid+1과 end로 놓고 다시 탐색
🍓 DP 로 해결 과정
import sys
print = sys.stdout.write
input = sys.stdin.readline
def sol(N, M):
if M == 0 :
return tree[0]
take = 0
for i in range(1,N+1):
if i == N :
break
take += (tree[i-1]-tree[i])*i
if take >= M:
break
if i == N :
height = int((sum(tree)-M)/N)
else:
height = tree[i] + (take-M)//i
return height
N, M = map(int, input().split())
tree = list(map(int,input().split()))
tree.sort(reverse=True)
print(str(sol(N,M)))
Tree 를 역순으로 정렬하였다.
각 트리의 높이는 각 군을 이룬다.
가령 Tree = [A, B, C, D, E, F, G] 가 있다고 할 때,
자르는 높이 h를 B로 하겠다고 하면, 상순이는 A-B 만큼 나무를 챙겨갈 것이다. (1군)
자르는 높이 h를 C로 하겠다고 하면, 상순이는 (A-B) + (B-C)*2 만큼 나무를 챙겨갈 것이다. (2군)
일반화 하면 다음과 같다.
\( Take = ( Tree[0] - Tree[1] )*1 + ( Tree[1] - Tree[2] )*2 + ... + ( Tree[n-1] - Tree[n] )*n \)
각 군에 대해서 상순이가 가져가야할 나무 양 M과 비교하여 M이 어떤 군에 속해있는지 찾는다.
가령 i군에 M이 속해 있다는 걸 알면, 높이는 다음 식으로 구할 수 있다.
\( height = Tree[i] + (Take - M)//i \)
i군일때, 상순이는 높이 1 당 i 만큼의 나무를 가져간다.
( 1군이면 높이 1당 나무 1, 10군이면 높이 1당 나무 10 만큼 )
바로 그러한 점을 이용해 식을 위와 같이 세웠다.
가령 Tree = [A, B, C] 일 때,
가져가야할 양 M이 (A-B) + (B-C)*2 + (C-B)*3 보다 많을 때는 D가 없기 때문에 위의 식으로 구할 수 없다.
따라서 그때는 \( height = int( (sum(Tree) - M)/N ) \) 으로 군수열과는 별도로 값을 구했다.
해석하면 다음과 같다. 높이 = ( 전체 나무의 양 - 가져갈 양 ) / (전체 나무 갯수)
상순이는 높이 1당 N만큼 나무를 가져가므로 다음의 식이 성립할 수 있었다.
'코딩테스트 > 백준 주제별' 카테고리의 다른 글
| [ 백준 브루트포스 ] 15686 치킨 배달 (0) | 2022.08.01 |
|---|---|
| [백준 그리디] 2138 전구와 스위치 (0) | 2022.07.26 |
| [백준 그래프이론] 1600 말이 되고픈 원숭이 (0) | 2022.07.11 |
| [백준 정렬] 10825 국영수 (0) | 2022.07.10 |
| [백준 위상정렬] 2623 음악프로그램 (0) | 2022.07.04 |
🥕 [ 백준 2850 ] 나무 자르기
문제 링크
url : https://www.acmicpc.net/problem/2805
2805번: 나무 자르기
첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000) 둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M보
www.acmicpc.net
🍒 문제 분석

필요한 양이 M 이라고 할 때
h 만큼의 높이를 잘라 잘리는 부분 ( 주황색 ) 의 합이 M보다 크면 되는 문제이다.
나무의 갯수는 100만개 까지, 나무의 높이는 20억 까지 있다. 그리고 제한 시간은 1초이다.
주어진 input은 크면서 시간이 적기 때문에 문제 풀이로서 떠올릴 수 있는 방법은 한정 되어있다.
1. 파라메트릭 서치
- 최적화 문제를 결정 문제로 바꾸어 해결하는 기법
( 결정 문제란 예, 아니오 로 답하는 문제를 말한다. ) - 원하는 조건을 만족하는 가장 알맞은 값을 찾는 문제
2. DP
- 최적화 문제를 푸는 방법
이코테 책에 따르면(202p),
높이가 10억일 때, 만약 이진 탐색으로 높이 H를 구하고자 한다면 대략 31번에 모든 경우의 수를 고려할 수 있다고 한다.
그리고 나무의 갯수가 최대 100만개라면, 이진 탐색으로 높이 H를 바꾸면서, 바꿀 때마다 모든 나무를 체크한다고 하면 최대 3,000만 번 정도의 연산으로 문제를 풀 수 있다고 한다. 3,000만 번의 연산이면 최악의 경우, 아슬아슬하게 약 2초가 걸린다고 한다.
본 문제에서는 주어진 조건이 1초여서, 좀 곤란해 보이는데... 잘 모르겠다 일단 풀어보자.
나는 먼저 DP로 문제를 해결하였고, 후에 파라메트릭 서치를 찾아보게 되었다.
본 리뷰는 파라 메트릭 서치를 먼저 한 후, DP에 대한 풀이 방법을 적고자한다.
( DP래 봤자 그냥 군수열 점화식 쓴거라서 별거 없다. )
🥑 파라메트릭 서치
import sys
input = sys.stdin.readline
write = sys.stdout.write
# 나무 수, 가져가려는 나무 길이
N, M = map(int, input().split())
# 나무 높이들
array = list(map(int,input().split()))
array.sort()
# 이진탐색
start = 1
end = max(array)
result = 0
while(start <= end):
total = 0
mid = (start + end)//2
for tree in array:
if tree > mid:
total += tree - mid
if total > M:
start = mid + 1
elif total < M :
end = mid - 1
else:
end = mid
break
print(str(end))
1. 높이 H를 임의로 중간 값(mid)으로 정하여 놓고 계산
2. 가져가는 양이 충분치 않으면 높이 H를 줄여야함.
높이 H 를 다시 start와 mid-1 의 중간값으로 놓고 다시 탐색
3. 가져가는 양이 너무 많다면 높이 H를 늘려야함
높이 H를 다시 mid+1과 end로 놓고 다시 탐색
🍓 DP 로 해결 과정
import sys
print = sys.stdout.write
input = sys.stdin.readline
def sol(N, M):
if M == 0 :
return tree[0]
take = 0
for i in range(1,N+1):
if i == N :
break
take += (tree[i-1]-tree[i])*i
if take >= M:
break
if i == N :
height = int((sum(tree)-M)/N)
else:
height = tree[i] + (take-M)//i
return height
N, M = map(int, input().split())
tree = list(map(int,input().split()))
tree.sort(reverse=True)
print(str(sol(N,M)))
Tree 를 역순으로 정렬하였다.
각 트리의 높이는 각 군을 이룬다.
가령 Tree = [A, B, C, D, E, F, G] 가 있다고 할 때,
자르는 높이 h를 B로 하겠다고 하면, 상순이는 A-B 만큼 나무를 챙겨갈 것이다. (1군)
자르는 높이 h를 C로 하겠다고 하면, 상순이는 (A-B) + (B-C)*2 만큼 나무를 챙겨갈 것이다. (2군)
일반화 하면 다음과 같다.
각 군에 대해서 상순이가 가져가야할 나무 양 M과 비교하여 M이 어떤 군에 속해있는지 찾는다.
가령 i군에 M이 속해 있다는 걸 알면, 높이는 다음 식으로 구할 수 있다.
i군일때, 상순이는 높이 1 당 i 만큼의 나무를 가져간다.
( 1군이면 높이 1당 나무 1, 10군이면 높이 1당 나무 10 만큼 )
바로 그러한 점을 이용해 식을 위와 같이 세웠다.
가령 Tree = [A, B, C] 일 때,
가져가야할 양 M이 (A-B) + (B-C)*2 + (C-B)*3 보다 많을 때는 D가 없기 때문에 위의 식으로 구할 수 없다.
따라서 그때는 으로 군수열과는 별도로 값을 구했다.
해석하면 다음과 같다. 높이 = ( 전체 나무의 양 - 가져갈 양 ) / (전체 나무 갯수)
상순이는 높이 1당 N만큼 나무를 가져가므로 다음의 식이 성립할 수 있었다.
'코딩테스트 > 백준 주제별' 카테고리의 다른 글
| [ 백준 브루트포스 ] 15686 치킨 배달 (0) | 2022.08.01 |
|---|---|
| [백준 그리디] 2138 전구와 스위치 (0) | 2022.07.26 |
| [백준 그래프이론] 1600 말이 되고픈 원숭이 (0) | 2022.07.11 |
| [백준 정렬] 10825 국영수 (0) | 2022.07.10 |
| [백준 위상정렬] 2623 음악프로그램 (0) | 2022.07.04 |
