[개념]
- 어떤 수열의 인접하는 두 항의 차로 이루어진 또 다른 수열
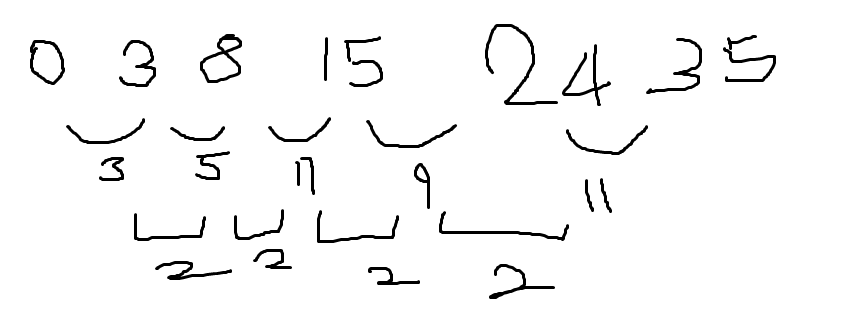
- 계차 수열을 이용해서 수열의 일반항을 구할 수 있다.
$$ \{b_n\}\ :\ 계차수열,\ \ \ \{a_n\}\ :\ 수열의 일반항$$
$$ b_1=a_{2}-a_{1} $$
$$ b_2=a_{3}-a_{2} $$
$$ ... $$
$$ ... $$
$$ b_{n-1} = a_{n}-a_{n-1} $$
계차수열 합 구할 때, n-1까지만 더함에 유의하자!!
$$ \therefore \underset{k=1}{\overset{n-1}{\Sigma}} b_k = a_n-a_1$$
$$ a_n = a_1 + \underset{k=1}{\overset{n-1}\Sigma}b_k $$
$$ \because b_n = b_1+(n-1)*d $$
$$ \underset{k=1}{\overset{n-1}{\Sigma}} b_k = (n-1)*(b_1 + b_{n-1})/2 $$
$$ \underset{k=1}{\overset{n-1}{\Sigma}} b_k = (n-1)*(2*b_1 + (n-2)*d )/2 $$
따라서 일반항은
$$ a_n = a_1 + (n-1)*(2*b_1 + (n-2)*d )/2 $$
위 예시에서 일반항은
$$a_n=0 + (n-1)*(6+(n-2)*2)/2$$
$$a_n= n^2 -1$$
[실습1] 공식 없이 계차수열과 수열 일반항 구하기
a1 = int(input('수열의 초항 입력 : '))
n = int(input('몇번째 항까지 궁금하세요? : '))
b1 = int(input('계차수열의 초항 입력 : '))
d = int(input('계차수열의 공차 입력 : '))
k = 1
while k <= n :
if k == 1 :
a = a1
b = b1
print('a의 {}번째 값은 {}'.format(k,a))
print('b의 {}번째 값은 {}'.format(k,b))
print('------------------------------')
k += 1
continue
a += b
b += d
print('a의 {}번째 값은 {}'.format(k,a))
print('b의 {}번째 값은 {}'.format(k,b))
print('------------------------------')
k += 1'''
수열의 초항 입력 : 3
몇번째 항까지 궁금하세요? : 7
계차수열의 초항 입력 : 4
계차수열의 공차 입력 : 2
a의 1번째 값은 3
b의 1번째 값은 4
------------------------------
a의 2번째 값은 7
b의 2번째 값은 6
------------------------------
a의 3번째 값은 13
b의 3번째 값은 8
------------------------------
a의 4번째 값은 21
b의 4번째 값은 10
------------------------------
a의 5번째 값은 31
b의 5번째 값은 12
------------------------------
a의 6번째 값은 43
b의 6번째 값은 14
------------------------------
a의 7번째 값은 57
b의 7번째 값은 16
------------------------------
'''[실습2] 공식 가지고 계차수열과 수열 일반항 구하기
a1 = int(input('수열의 초항 입력 : '))
n = int(input('몇번째 항까지 궁금하세요? : '))
b1 = int(input('계차수열의 초항 입력 : '))
d = int(input('계차수열의 공차 입력 : '))
b = b1 + d*(n-1)
a = a1 + (n-1)*(2*b1+d*(n-2))//2
print('{}번째 계수수열과 수열의 일반항은 {} 와 {} 입니다.'.format(n,b,a))코드'''
수열의 초항 입력 : 3
몇번째 항까지 궁금하세요? : 7
계차수열의 초항 입력 : 4
계차수열의 공차 입력 : 2
7번째 계수수열과 수열의 일반항은 16 와 57 입니다.
'''
'기초 수학' 카테고리의 다른 글
| [기초수학] 팩토리얼 (0) | 2022.04.27 |
|---|---|
| [기초수학] 피보나치 수열 (0) | 2022.04.27 |
| [기초 수학] 등비 수열 (0) | 2022.04.27 |
| [기초수학] 등차 수열 (0) | 2022.04.26 |
| [기초수학] 진법 (0) | 2022.04.26 |
[개념]
- 어떤 수열의 인접하는 두 항의 차로 이루어진 또 다른 수열
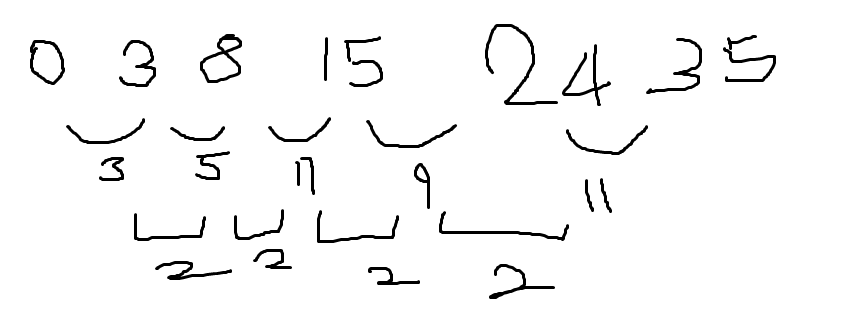
- 계차 수열을 이용해서 수열의 일반항을 구할 수 있다.
$$ \{b_n\}\ :\ 계차수열,\ \ \ \{a_n\}\ :\ 수열의 일반항$$
$$ b_1=a_{2}-a_{1} $$
$$ b_2=a_{3}-a_{2} $$
$$ ... $$
$$ ... $$
$$ b_{n-1} = a_{n}-a_{n-1} $$
계차수열 합 구할 때, n-1까지만 더함에 유의하자!!
$$ \therefore \underset{k=1}{\overset{n-1}{\Sigma}} b_k = a_n-a_1$$
$$ a_n = a_1 + \underset{k=1}{\overset{n-1}\Sigma}b_k $$
$$ \because b_n = b_1+(n-1)*d $$
$$ \underset{k=1}{\overset{n-1}{\Sigma}} b_k = (n-1)*(b_1 + b_{n-1})/2 $$
$$ \underset{k=1}{\overset{n-1}{\Sigma}} b_k = (n-1)*(2*b_1 + (n-2)*d )/2 $$
따라서 일반항은
$$ a_n = a_1 + (n-1)*(2*b_1 + (n-2)*d )/2 $$
위 예시에서 일반항은
$$a_n=0 + (n-1)*(6+(n-2)*2)/2$$
$$a_n= n^2 -1$$
[실습1] 공식 없이 계차수열과 수열 일반항 구하기
a1 = int(input('수열의 초항 입력 : '))
n = int(input('몇번째 항까지 궁금하세요? : '))
b1 = int(input('계차수열의 초항 입력 : '))
d = int(input('계차수열의 공차 입력 : '))
k = 1
while k <= n :
if k == 1 :
a = a1
b = b1
print('a의 {}번째 값은 {}'.format(k,a))
print('b의 {}번째 값은 {}'.format(k,b))
print('------------------------------')
k += 1
continue
a += b
b += d
print('a의 {}번째 값은 {}'.format(k,a))
print('b의 {}번째 값은 {}'.format(k,b))
print('------------------------------')
k += 1'''
수열의 초항 입력 : 3
몇번째 항까지 궁금하세요? : 7
계차수열의 초항 입력 : 4
계차수열의 공차 입력 : 2
a의 1번째 값은 3
b의 1번째 값은 4
------------------------------
a의 2번째 값은 7
b의 2번째 값은 6
------------------------------
a의 3번째 값은 13
b의 3번째 값은 8
------------------------------
a의 4번째 값은 21
b의 4번째 값은 10
------------------------------
a의 5번째 값은 31
b의 5번째 값은 12
------------------------------
a의 6번째 값은 43
b의 6번째 값은 14
------------------------------
a의 7번째 값은 57
b의 7번째 값은 16
------------------------------
'''[실습2] 공식 가지고 계차수열과 수열 일반항 구하기
a1 = int(input('수열의 초항 입력 : '))
n = int(input('몇번째 항까지 궁금하세요? : '))
b1 = int(input('계차수열의 초항 입력 : '))
d = int(input('계차수열의 공차 입력 : '))
b = b1 + d*(n-1)
a = a1 + (n-1)*(2*b1+d*(n-2))//2
print('{}번째 계수수열과 수열의 일반항은 {} 와 {} 입니다.'.format(n,b,a))코드'''
수열의 초항 입력 : 3
몇번째 항까지 궁금하세요? : 7
계차수열의 초항 입력 : 4
계차수열의 공차 입력 : 2
7번째 계수수열과 수열의 일반항은 16 와 57 입니다.
'''
'기초 수학' 카테고리의 다른 글
| [기초수학] 팩토리얼 (0) | 2022.04.27 |
|---|---|
| [기초수학] 피보나치 수열 (0) | 2022.04.27 |
| [기초 수학] 등비 수열 (0) | 2022.04.27 |
| [기초수학] 등차 수열 (0) | 2022.04.26 |
| [기초수학] 진법 (0) | 2022.04.26 |
