Average Orientation Similarity

개요

• KITTI 방향 검출 성능에 대한 공식 평가 지표이다.
• 출처 : https://towardsdatascience.com/orientation-estimation-in-monocular-3d-object-detection-f850ace91411

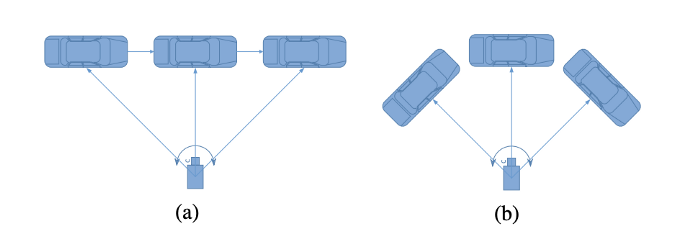
• a 에서 자동차의 global orientation은 모두 오른쪽을 향하고 있지만, 자동차가 왼쪽에서 오른쪽으로 움직일 때 local orientation 과 외견은 달라집니다.
• b 에서 자동차의 global orientation은 다르지만, 카메라 좌표의 local orientation과 외견은 모두 변하지 않습니다.

 

( a )의 예시

KITTI 에서는 roll과 pitch에 대해 0을 가정하기 때문에, 방향은 단순히 yaw 로 표현된다.

 

Local to Global Yaw

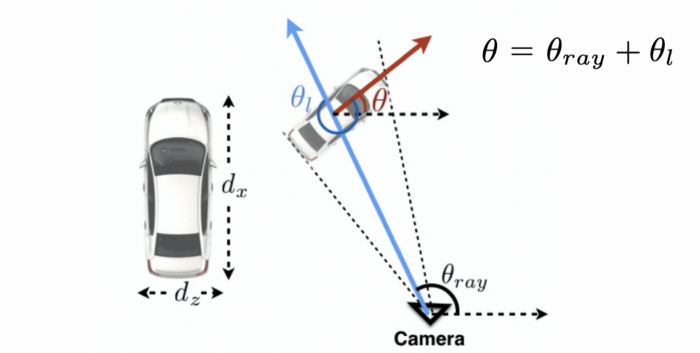
• 카메라와 객체 간의 Ray Direction을 알고 있어야 local yaw 로부터 global yaw 를 알 수 있습니다.
• Bounding Box의 포인트 값들과 Intrinsic Matrix ( Focal Point and Focal Length) 를 알고 있어야 Ray Direction을 알 수 있습니다.
• Bounding Box와 관련하여 선택 가능한 변수들
  • center of detector boxes (may be truncated)
  • center of amodal boxes (with guessed extension for occluded or truncated object)
  • projection of 3D bounding box on the image (can be obtained from lidar 3D bounding box ground truth)
  • bottom center of 2D bounding box (which is often assumed to be on the ground)

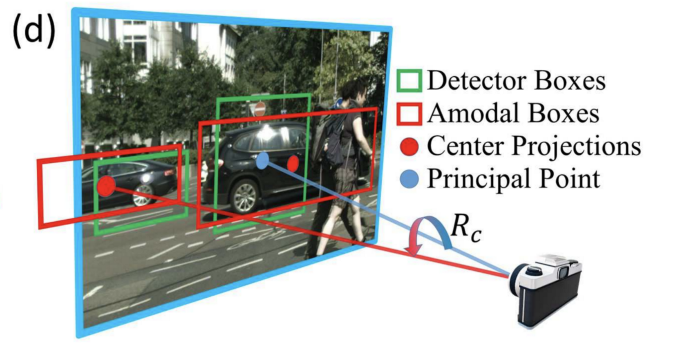
차량이 정말로 가깝거나 심하게 잘리거나(truncated), 시야 밖을 벗어나지 않는 이상(occluded) 위의 방법을 통해 약 1 ~ 2 도 정도 떨어진 각도 추정을 산출할 수 있을 것입니다.

 

AOS 구하기

KITTI 에서는 다음의 두가지 각도를 제공합니다.

• alpha : Observation Angle of Object, ranging [-pi, pi]
• rotation_y : Rotation ry arround Y axis in camera coordinates [-pi, pi]

위 두 각도는 local(allocentric) yaw와 global(egocentric) yaw 입니다.

라이더 데이터를 기반으로 한 3D Bounding Box ground truth 에서 추정한 결과일 것으로 보입니다.

이를 통해 2D 이미지에서 각도 추정을 쉽게 수행할 수 있습니다.

 

https://www.cvlibs.net/publications/Geiger2012CVPR.pdf

 

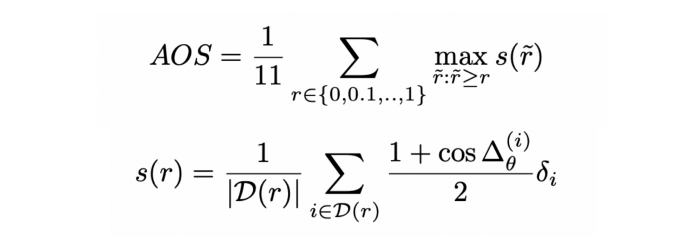
3D RCNN 에 의해 대중화된, Average Angular Error (AAE) 라는 매트릭 또한 있습니다.

 

https://openaccess.thecvf.com/content_cvpr_2018/papers/Kundu_3D-RCNN_Instance-Level_3D_CVPR_2018_paper.pdf

 

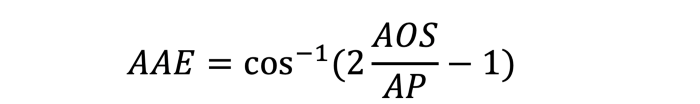
한 발짝 더 나아가기

• local image patch로부터 the local (allocentric) orientation (yaw)를 추정할 수 있습니다.
• local image patch로부터 the global (egocentric) orientation (yaw)를 추정할 수 없습니다.
• 카메라의 Intrinsic와 global information of the image patch를 사용하면 local yaw를 global yaw로 전환 가능합니다.
• The regression of viewpoint orientation 은 딥러닝에서 가장 어려운 회귀 문제 중 하나 입니다.
  https://towardsdatascience.com/anchors-and-multi-bin-loss-for-multi-modal-target-regression-647ea1974617

Multimodal Regression — Beyond L1 and L2 Loss